Применение производной в других науках методическая разработка по алгебре (10 класс) на тему. Применение производной, проектная деятельность на уроках математики (10 класс) Использование производной на практике

Министерство образования Саратовской области

Государственное автономное профессиональное образовательное учреждение Саратовской области «Энгельсский политехникум»

ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ В РАЗНИЧНЫХ ОБЛАСТЯХ НАУКИ

Выполнила: Саркулова Нургуля Сергеевна

студентка группы КШИ-216/15

(Конструирование, моделирование и

технология швейных изделий)

Научный руководитель:

Вербицкая Елена Вячеславовна

преподаватель математики ГАПОУ СО

«Энгельсский политехникум»

2016

Введение

Роль математики в различных областях естествознания очень велика. Недаром говорят «Математика – царица наук, физика ее правая рука, химия – левая».

Предмет исследования – производная.

Ведущая цель - показать значимость производной не только в математике, но и в других науках, её важность в современной жизни.

Дифференциальное исчисление – это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники.

Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д.

Ключевой и тематический вопросы данного реферата:

1. История возникновения производной.

2. Зачем изучать производные функций?

3. Где используются производные?

4. Применение производных в физике, химии, биологии и других науках.

5. Выводы

Я решила написать работу на тему «Применение производной в различных областях науки», потому что считаю эту тему очень интересной, полезной и актуальной.

В своей работе я расскажу о применении дифференцирования в различных областях науки, таких как химия, физика, биология, география и т. д. Ведь все науки неразрывно связаны между собой, что очень хорошо видно на примере рассматриваемой мною темы.

Применение производной в различных областях науки

Из курса алгебры старших классов мы уже знаем, что производная - это предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.

Действие нахождения производной называется её дифференцированием, а функцию, имеющую производную в точке х, называют дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке промежутка, называется дифференцируемой в этом промежутке.

Честь открытия основных законов математического анализа принадлежит английскому физику и математику Исааку Ньютону и немецкому математику, физику, философу Лейбницу.

Ньютон ввел понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.

Физический смысл производной: производная функции y = f (x ) в точке x 0 – это скорость изменения функции f (x ) в точке x 0 .

Лейбниц пришёл к понятию производной, решая задачу проведения касательной к производной линии, объяснив этим ее геометрический смысл.

Геометрический смысл производной состоит в том, что производная функция в точке x 0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x 0 .

Термин производная и современные обозначения y " , f " ввёл Ж.Лагранж в 1797г.

Российский математик 19 века Панфутий Львович Чебышев говорил, что «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека, например, как располагать своими средствами для достижения наибольшей выгоды».

С такими задачами в наше время приходится иметь дело представителям самых разных специальностей:

Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;

Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей;

Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.

При изучении любой темы у учеников возникает вопрос: «Зачем нам это надо?» Если ответ удовлетворит любопытство, то можно говорить о заинтересованности учеников. Ответ для темы «Производная» можно получить, зная, где используются производные функций.

Чтобы ответить на этот вопрос, можно перечислить некоторые дисциплины и их разделы, в которых применяются производные.

Производная в алгебре:

1. Касательная к графику функции

Касательная к графику функции f, дифференцируемой в точке x о , - это прямая, проходящая через точку (x о ; f (x о )) и имеющая угловой коэффициент f ′(x о ).

y = f (x о ) + f ′(x о ) (x – x о )

2. Поиск промежутков возрастания и убывания функции

Функция y=f(x) возрастает на интервале X , если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Функция y=f(x) убывает на интервале X , если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.

3. Поиск точек экстремума функции

Точку называют точкой максимума функции y=f(x) , если для всех x . Значение функции в точке максимума называют максимумом функции и обозначают .

Точку называют точкой минимума функции y=f(x) , если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают .

Под окрестностью точки понимают интервал , где - достаточно малое положительное число.

Точки минимума и максимума называют точками экстремума , а значения функции, соответствующие точкам экстремума, называют экстремумами функции .

4. Поиск промежутков выпуклости и вогнутости функции

График функции , является на этом интервале выпуклым , лежит не выше любой своей касательной (рис. 1).

График функции , дифференцируемой на интервале , является на этом интервале вогнутым , если график этой функции в пределах интервала лежит не ниже любой своей касательной (рис. 2).

Точкой перегиба графика функции называется точка , разделяющая промежутки выпуклости и вогнутости.

5. Поиск точек изгиба функции

Производная в физике:

1. Скорость как производная пути

2. Ускорение как производная скорости a =

3. Скорость распада радиоактивных элементов 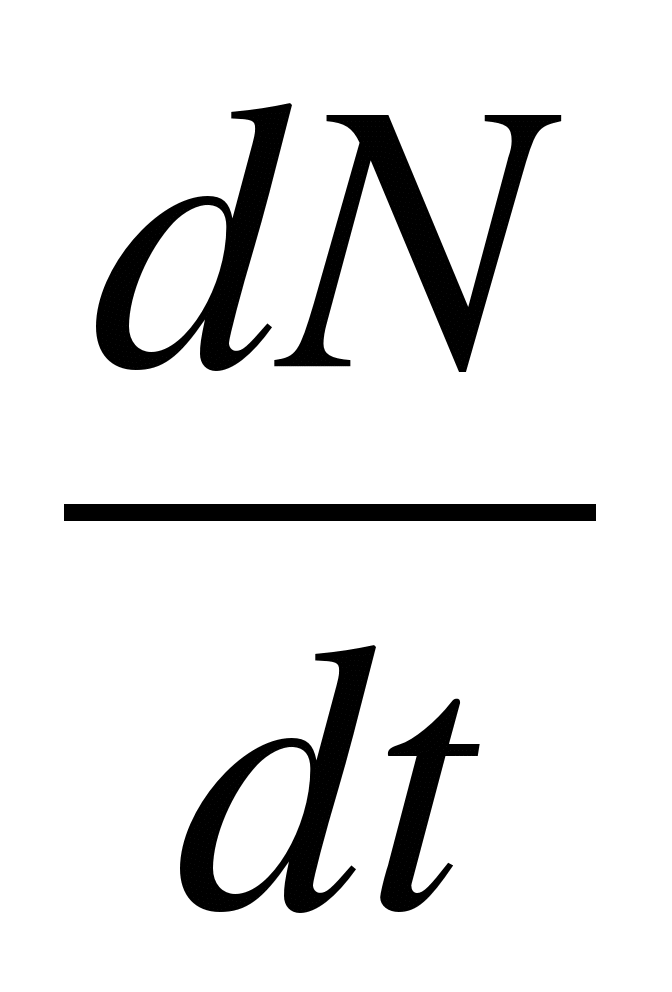= - λN

А так же в физике производную применяют для вычисления:

Скорости материальной точки

Мгновенной скорости как физический смысл производной

Мгновенное значение силы переменного тока

Мгновенное значение ЭДС электромагнитной индукции

Максимальную мощность

Производная в химии:

И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.

Производную в химии используют для определения очень важной вещи – скорости химической реакции, одного из решающих факторов, который нужно учитывать во многих областях научно-производственной деятельности . V (t) = p ‘(t)

в-ва в момент времени t 0

p = p(t 0 )

Функция

Интервал времени

∆t = t– t 0

Приращение аргумента

Изменение количества в-ва

∆p= p(t 0 + ∆ t) – p(t 0 )

Приращение функции

Средняя скорость химической реакции

∆p/∆t

Отношение приращёния функции к приращёнию аргумента

Производная в биологии:

Популяция – это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.

Р = х‘ (t)

Производная в географии:

1. Некоторые значения в сейсмографии

2. Особенности электромагнитного поля земли

3. Радиоактивность ядерно- геоифзичексих показателей

4.Многие значения в экономической географии

5.Вывести формулу для вычисления численности населения на территории в момент времени t.

у’= к у

Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N(t) .Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует

Производная в электротехнике:

В наших домах, на транспорте, на заводах: всюду работает электрический ток. Под электрическим током понимают направленное движение свободных электрически заряженных частиц.

Количественной характеристикой электрического тока является сила тока.

В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.

В электротехнике в основном используется работа переменного тока.

Электрический ток, изменяющийся со временем, называют переменным. Цепь переменного тока может содержать различные элементы: нагревательные приборы, катушки, конденсаторы.

Получение переменного электрического тока основано на законе электромагнитной индукции, формулировка которого содержит производную магнитного потока.

Производная в экономике:

Экономика – основа жизни, а в ней важное место занимает дифференциальное исчисление – аппарат для экономического анализа. Базовая задача экономического анализа – изучение связей экономических величин в виде функций.

Производная в экономике решает важные вопросы:

1. В каком направлении изменится доход государства при увеличении налогов или при введении таможенных пошлин?

2. Увеличится или уменьшится выручка фирмы при увеличение цены на её продукцию?

Для решения этих вопросов нужно построить функции связи входящих переменных, которые затем изучаются методами дифференциального исчисления.

Также с помощью экстремума функции (производной) в экономике можно найти наивысшую производительность труда, максимальную прибыль, максимальный выпуск и минимальные издержки.

ВЫВОД: производная успешно применяется при решении различных прикладных задач в науке, технике и жизни

Как видно из вышеперечисленного применение производной функции весьма многообразно и не только при изучении математики, но и других дисциплин. Поэтому можно сделать вывод, что изучение темы: «Производная функции» будет иметь своё применение в других темах и предметах.

Мы убедились в важности изучения темы "Производная", ее роли в исследовании процессов науки и техники, в возможности конструирования по реальным событиям математические модели, и решать важные задачи.

“Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей”.

Так сказал американский математик Морис Клайн.

Список используемой литературы:

1. Богомолов Н.В., Самойленко И.И. Математика. - М.: Юрайт, 2015.

2. Григорьев В.П., Дубинский Ю.А, Элементы высшей математики. - М.: Академия, 2014.

3. Баврин И.И. Основы высшей математики. - М.: Высшая школа, 2013.

4. Богомолов Н.В. Практические занятия по математике. - М.: Высшая школа, 2013.

5. Богомолов Н.В. Сборник задач по математике. - М.: Дрофа, 2013.

6. Рыбников К.А. История математики, «Издательство Московского университета», М, 1960.

7. Виноградов Ю.Н., Гомола А.И., Потапов В.И., Соколова Е.В. – М.: Издательский центр «Академия», 2010

8 . Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия. – М.: Издательский центр «Академия», 2016

Периодические источники:

Газеты и журналы: «Математика», «Открытый урок»

Использование ресурсов сети Интернет, электронных библиотек:

www:egetutor.ru

matematika-na5.norod.ru

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

Всероссийский конкурс исследовательских работ учащихся

"ЮНОСТЬ, НАУКА, КУЛЬТУРА”

Творческая работа

Тема: "Применение производной в различных областях науки"

Калужский Михаил МБОУ "СОШ № 60 им. В. Завьялова"

Научный руководитель:

Минина М.Н.

г. Барнаул 2013/2014

Оглавление

• Введение
• Глава I
• 1.1 Исторические сведения
• Глава II . Применение физического смысла производной при решении физических задач
• 1.1 Производная в механике
• Глава III . Решение химических и биологических задач с помощью производной
• 3.1 Производная в химии
• 3.2 Производная в биологии
• Глава IV . Решение задач с географическим, экономическим содержанием
• 4.1 Производная в географии
• 4.2 Производная в экономике
• Заключение
• Приложение

Введение

Тема "Производная функции" считается самой сложной в курсе школьной математики. Однако, "сложность" этой темы заключается в непонимании учащимися её нужности. Область применения производной остается непознанной даже студентам вузов. В связи с этим я решил провести опрос.

Данный опрос показал, что большинство людей не имеют полного представления о производной и обширной области её применения. Моя работа раздвигает рамки обыденного, она дает возможность разобраться в теме "производная функции", понять что производная встречается повсюду и очень важно знать что это такое и как это устроено.

производная функция математика наука

Глава I

1.1 Исторические сведения

Производная - одно из фундаментальных понятий математики. Оно возникло в 18 веке. Независимо друг от друга И. Ньютон и Г. Лейбниц разработали теорию дифференциального исчисления.

Исаак Ньютон (1643-1727) - один из создателей дифференциального исчисления. Главный его труд - "Математические начала натуральной философии". - оказал колоссальное влияние на развитие естествознания, стал поворотным пунктом в истории естествознания.

Ньютон ввёл понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.

Г.В. Лейбниц. (1646-1716) - создатель Берлинской академии наук. Основоположник дифференциального исчисления, ввёл большую часть современной символики математического анализа.

Лейбниц пришёл к понятию производной, решая задачу проведения касательной к произвольной линии, объяснив этим ее геометрический смысл. В самом деле для любой функции y=f (x) в системе координат, на ее области определения можно построить график. Если взять точку на оси абсцисс то, соответственно этой точки можно найти точку на графике функции. В этой точке может быть построена касательная, которая образует с положительным направлением оси абсцисс угол б.

Но это не говорит о том, …

…что до них эти вопросы не изучались. Задолго до этого Архимед (287 до н.э. - 212 до н. э) не только решил задачу на построение касательной к такой сложной кривой, как спираль, применяя при этом предельные переходы, но и сумел найти максимум функции.

Эпизодически понятие касательной встречалось в работах итальянского математика И. Тартальи (1499-1557).

В 17в. на основе учения Г. Галилея (1564-1642) активно развилась кинематическая концепция производной. Понятие производной встречается уже у Р. Декарта (1596-1650), французского математика Ж. Роберваля (1602-1675), английского учёного Д. Грегори (1638-1675), в работах И. Барроу (1630-1677).

Большой вклад в изучение дифференциального исчисления внесли Лопиталь (1661-1704), Бернулли (1744-1807), Лагранж (1736-1813), Гаусс (1777-1855), Коши (1789-1857). Необходимо сказать, что ни Ньютон ни Лагранж не дали четкого определения производной. Впервые определение производной было сформулировано Коши, и именно это определение стало общепринятым и в настоящее время используется почти во всех курсах анализа.

Глава II. Применение физического смысла производной при решении физических задач

Применение производной в физике очень обширно. Рассмотрим несколько примеров применения производной в физических задачах.

1.1 Производная в механике

Механическое движение - это изменение положения тела в пространстве относительно других тел с течением времени.

Основной характеристикой механического движения служит скорость.

Алгоритм нахождения скорости тела с помощью производной.

Если закон движения тела задан уравнением s = s (t), то для нахождения мгновенной скорости тела в какой-нибудь определенный момент времени надо:

1. Найти производную s" = f " (t).

2. Подставить в полученную формулу заданное значение времени.

Задание. Автомобиль приближается к мосту со скоростью 72 км/ч. У моста висит дорожный знак "36 км/ч". За 7 сек до въезда на мост, водитель нажал на тормозную педаль. С разрешаемой ли скоростью автомобиль въехал на мост, если тормозной путь определяется формулой s=20t-tІ

Да, т.к. скорость через 7 сек. будет равна 6м/с (21,6 км/ч).

1.2 Производная в электротехнике

В наших домах, на транспорте, на заводах: всюду работает электрический ток.

Под электрическим током понимают направленное движение свободных электрически заряженных частиц.

Количественной характеристикой электрического тока является сила тока.

В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.

В электротехнике в основном используется работа переменного тока.

Электрический ток, изменяющийся со временем, называют переменным. Цепь переменного тока может содержать различные элементы: нагревательные приборы, катушки, конденсаторы.

Получение переменного электрического тока основано на законе электромагнитной индукции, формулировка которого содержит производную магнитного потока.

Задание.

Заряд, протекающий через проводник, меняется по закону

Найти силу тока в момент времени t=5 cек.

Сила тока равна 2 А

Сила есть производная работы по перемещению,

т.е. F=A / (x )

Теплоемкость - есть производная теплоты по температуре, т.е. C (t) = Q / (t)

d (l ) =m / (l ) - линейная плотность

K (t) = l / (t) - коэффициент линейного расширения

щ (t) = ц / (t) - угловая скорость

а (t) = щ / (t) - угловое ускорение

N (t) = A / (t) - мощность

Задание : теплота .

1. Пусть Q (t) количество теплоты, которое необходимо для нагревания тела массой 1 кг от 0 0 С до температуры t 0 (по Цельсию), известно, что в диапазоне 0 0 до 95 0 , формула Q (t) = 0,396t+2,08110 -3 t 2 -5,02410 -7 t 3 дает хорошее приближение к истинному значению. Найдите, как зависит теплоёмкость воды от t.

Решение . C (t) = Q / (t) = 0,396 + 4,162*10 - 3 t - 15,072*10 - 7 t 2

Глава III. Решение химических и биологических задач с помощью производной

3.1 Производная в химии

И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.

Химия - это наука о веществах, о химических превращениях веществ.

Химия изучает закономерности протекания различных реакций.

Скоростью химической реакции называется изменение концентрации реагирующих веществ в единицу времени.

Так как скорость реакции v непрерывно изменяется в ходе процесса, ее обычно выражают производной концентрации реагирующих веществ по времени.

Если C (t ) - закон изменения количества вещества, вступившего в химическую реакцию, то скорость v (t ) химической реакции в момент времени t равна производной:

Предел этого отношения при стремлении Дt к нулю - есть скорость химической реакции в данный момент времени V (t) = c ` (t)

Найти скорость реакции в момент времени t = 10 сек, если концентрация исходного продукта меняется по закону

3.2 Производная в биологии

Популяция - это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.

Задача по биологии.

По известной зависимости численности популяции x (t) определить относительный прирост в момент времени t.

Глава IV. Решение задач с географическим, экономическим содержанием

4.1 Производная в географии

Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N (t), . Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует.

Выведем формулу для вычисления численности населения на ограниченной территории в момент времени t.

Пусть у = у (t) - численность населения.

Рассмотрим прирост населения за t = t-t 0

y = k y t,

где к = к р - к с - коэффициент прироста (к р - коэффициент рождаемости,

к с - коэффициент смертности)

y: t=k y

При t0 получим lim y/ t=у"

у"= к у

4.2 Производная в экономике

Современный экономист должен хорошо владеть количественными методами анализа. К такому выводу нетрудно прийти практически с самого начала изучения экономической теории. При этом важны как знания традиционных математических курсов (математический анализ, линейная алгебра, теория вероятностей), так и знания, необходимые непосредственно в практической экономике и экономических исследованиях (математическая и экономическая статистика, теория игр, эконометрика и др.).

Математика является не только орудием количественного расчета, но также методом точного исследования. Она служит средством предельно четкой и ясной формулировки экономических понятий и проблем.

Ф. Энгельс в своё время заметил, что "лишь дифференциальное исчисление даёт естествознанию возможность изображать математически не только состояния, но и процессы: движение". Поэтому целью моей работы является выяснить, каков экономический смысл производной, какие новые возможности для экономических исследований открывает дифференциальное исчисление, а также исследовать применение производной при решении различных видов задач по экономической теории.

П (t) = х / (t) - производительность труда, где х (t) - объем продукции J (x) = y / (x) - предельные издержки производства, где y - издержки производства в зависимости от объема выпускаемой продукции x.

Задание.

Оборот предприятия за истекший год описывается через функцию U (t) =0,15tі - 2tІ + 200, где t - месяцы, U-миллионы.

Исследуйте оборот предприятия за 9 и 10 месяцы.

Решение. Исследуем оборот предприятия с помощью производной: U" (t) =0,45tІ - 4t

Меньший оборот был на девятом месяце - 0,45. На 10 месяце - 5.

Заключение

Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д. Мы убедились в важности изучения темы "Производная", ее роли в исследовании процессов науки и техники, в возможности конструирования по реальным событиям математические модели, и решать важные задачи.

Список используемых источников

1. http://ru. wikipedia.org/

2. http://www.calameo.com/

3. http://rudocs. exdat.com/

4. http://www.rae.ru/

5. А. Фуше "Педагогики математики"

Приложение

Го м тфрид Ви м льгельм Ле м йбниц (нем. Gottfried Wilhelm Leibniz); 21 июня (1 июля) 1646 - 14 ноября 1716) - немецкий философ, логик,математик, механик, физик, юрист, историк, дипломат, изобретатель и языковед. Основатель и первый президент Берлинской Академии наук, иностранный член Французской Академии наук

Сэр Исаа м к Нью м тон (англ. Sir Isaac Newton, 4 января 1643 года - 31 марта 1727 года) - английский физик, математик, механик и астроном, один из создателей классической физики. Автор фундаментального труда "Математические начала натуральной философии", в котором он изложил закон всемирного тяготения и три закона механики, ставшие основой классической механики. Разработал дифференциальное и интегральное исчисления, теорию цвета и многие другие математические и физические теории.

Размещено на Allbest.ru

Подобные документы

Понятие производной, правила её применения, геометрический и физический смысл производной. Применение производной в науке и технике и о решении задач в этой области. Актуальность дифференциального исчисления в связи с научно-техническим прогрессом.

реферат , добавлен 17.05.2009


Определение производной, понятие интеграла и определение предела функции. Дифференцирование и применение производной к решению задач. Исследование функции, вычисление интегралов и доказательство неравенств. Порядок вычисления пределов, Правило Лопиталя.

курсовая работа , добавлен 01.06.2014


Производная функция. Касательная к кривой. Геометрический смысл производной. Производные от элементарных функций. Изучение функций с помощью производной. Максимум и минимум функции. Точки перегиба. Дифференциал.

статья , добавлен 11.01.2004


Осуществление интерполяции с помощью полинома Ньютона. Уточнение значения корня на заданном интервале тремя итерациями и нахождение погрешности вычисления. Применение методов Ньютона, Сампсона и Эйлера при решении задач. Вычисление производной функции.

контрольная работа , добавлен 02.06.2011


Предел отношения приращения функции к приращению независимого аргумента, когда приращение аргумента стремится к нулю. Обозначения производной. Понятие дифференцирования функции производной и ее геометрический смысл. Уравнение касательной к кривой.

презентация , добавлен 21.09.2013


Геометрический смысл производной. Анализ связи между непрерывностью и дифференцируемостью функции. Производные основных элементарных функций. Правила дифференцирования. Нахождение производной неявно заданной функции. Логарифмическое дифференцирование.

презентация , добавлен 14.11.2014


Поиск производной сложной функции как равной производной функции по промежуточному аргументу, умноженной на его производную по независимой переменной. Теорема о связи бесконечно малых величин с пределами функций. Правило дифференцирования сложной функции.

презентация , добавлен 21.09.2013


Определение производной функции, геометрический смысл ее приращения. Геометрический смысл заданного отношения. Физический смысл производной функции в данной точке. Число, к которому стремится заданное отношение. Анализ примеров вычисления производной.

презентация , добавлен 18.12.2014


Некоторые применения производной. Использование основных теорем дифференциального исчисления к доказательству неравенств. Первообразная и интеграл в задачах элементарной математики. Монотонность интеграла. Некоторые классические неравенства.

курсовая работа , добавлен 11.01.2004


Понятие производной, ее геометрический и физический смысл, дифференциал. Исследование функций и построение графиков. Разложение на множители, упрощение выражений. Решение неравенств, систем уравнений и доказательство тождеств. Вычисление пределов функции.

Чайкин Семён, Майсак Кирилл, Залогина Анастасия, Шахзадова Анна

Данная разработка содержит презентацию по теме "Применение производной в химии и биологии". В ходе проектной деятельности была выдвинута гипотеза о том, что производная находит свое применение в этих областях науки. В ходе исследовательской работы было выяснено, какова роль производной в таких науках как химия и биология, где и при решении каких задач она находит свое применение. В результате проделанной работы пришли к выводу, что гипотеза действительно подтвердилась.

Скачать:

Предварительный просмотр:

https://accounts.google.com

Подписи к слайдам:

Гипотеза:

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Применение производной в химии и биологии Работу выполнили ученики 11В класса МБОУ СОШ №6: Чайкин Семен, Майсак Кирилл, Залогина Анастасия, Шахзадова Анна г. Ставрополь, 2014 год

Гипотеза:

И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств. Химия – это наука о веществах, о химических превращениях веществ. Химия изучает закономерности протекания различных реакций Скоростью химической реакции называется изменение концентрации реагирующих веществ в единицу времени. Применение производной в химии и биологии Определение скорости химической реакции

Зачем нужна производная в реакциях? Так как скорость реакции v непрерывно изменяется в ходе процесса, ее обычно выражают производной концентрации реагирующих веществ по времени.

Формула производной в химии Если C (t) – закон изменения количества вещества, вступившего в химическую реакцию, то скорость v (t) химической реакции в момент времени t равна производной:

Определение скорости реакции Предел отношения приращённой функции к приращённому аргументу при стремлении Δt к нулю - есть скорость химической реакции в данный момент времени

Задача по химии: Пусть количество вещества, вступившего в химическую реакцию задается зависимостью: С (t) = t 2 /2 + 3 t –3 (моль) Найти скорость химической реакции через 3 секунды. Решение: v (t) = С ‘(t) ; v (t) = t + 3; v (3) = 3+3 = 6. Ответ: 6 моль\с.

Биологический смысл производной Пусть зависимость между числом особей популяции микроорганизмов у и временем t её размножения задана уравнением: у = x (t). Пусть ∆ t - промежуток времени от некоторого начального значения t до t +∆ t . Тогда у + ∆у = x (t +∆ t) - новое значение численности популяции, соответствующее моменту t +∆ t , а ∆ y + x (t + ∆ t)- x (t) - изменение числа особей организмов. Отношение является средней скоростью размножения или, как принято говорить, средней производительностью жизнедеятельности популяции. Вычисляя, получаем y ‘ = P (t) = x ‘ (t) , или производительность жизнедеятельности популяции в момент времени t .

Популяция – это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.

Пример Пусть популяция бактерий в момент t (с) насчитывает x(t) особей. . Найти скорость роста популяции: а) в произвольный момент t , б) в момент t = 1 c . Решение: P = x’(t) = 200t; P(1) = 200 (о/с). Ответ: 200 о/с.

Заключение Понятие производной очень важно в химии и в биологии, особенно при определении скорости течения реакции.

Вывод: Дифференциальное исчисление- это описание окружающего нас мира, выполненное на математическом языке. Производная - одно из самых важных понятий математического анализа. Знание производной помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки, техники и жизни.

Роль математики в различных областях естествознания очень велика. Недаром говорят «Математика – царица наук, физика ее правая рука, химия – левая».

Предмет исследования – производная.

Ведущая цель - показать значимость производной не только в математике, но и в других науках, её важность в современной жизни.

Скачать:

Предварительный просмотр:

Министерство образования Саратовской области

Государственное автономное профессиональное образовательное учреждение Саратовской области «Энгельсский политехникум»

ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ В РАЗНИЧНЫХ ОБЛАСТЯХ НАУКИ

Выполнила: Вербицкая Елена Вячеславовна

Преподаватель математики ГАПОУ СО

«Энгельсский политехникум»

2016

Введение

Роль математики в различных областях естествознания очень велика. Недаром говорят «Математика – царица наук, физика ее правая рука, химия – левая».

Предмет исследования – производная.

Ведущая цель - показать значимость производной не только в математике, но и в других науках, её важность в современной жизни.

Дифференциальное исчисление – это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники.

Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д.

Ключевой и тематический вопросы данного реферата:

1. История возникновения производной.

2. Зачем изучать производные функций?

3. Где используются производные?

4. Применение производных в физике, химии, биологии и других науках.

5. Выводы

Я решила написать работу на тему «Применение производной в различных областях науки», потому что считаю эту тему очень интересной, полезной и актуальной.

В своей работе я расскажу о применении дифференцирования в различных областях науки, таких как химия, физика, биология, география и т. д. Ведь все науки неразрывно связаны между собой, что очень хорошо видно на примере рассматриваемой мною темы.

Применение производной в различных областях науки

Из курса алгебры старших классов мы уже знаем, что производная - это предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.

Действие нахождения производной называется её дифференцированием, а функцию, имеющую производную в точке х, называют дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке промежутка, называется дифференцируемой в этом промежутке.

Честь открытия основных законов математического анализа принадлежит английскому физику и математику Исааку Ньютону и немецкому математику, физику, философу Лейбницу.

Ньютон ввел понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.

Физический смысл производной: производная функции y=f(x) в точке x 0 – это скорость изменения функции f(x) в точке x 0 .

Лейбниц пришёл к понятию производной, решая задачу проведения касательной к производной линии, объяснив этим ее геометрический смысл.

Геометрический смысл производной состоит в том, что производная функция в точке x 0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x 0 .

Термин производная и современные обозначения y" , f " ввёл Ж.Лагранж в 1797г.

Российский математик 19 века Панфутий Львович Чебышев говорил, что «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека, например, как располагать своими средствами для достижения наибольшей выгоды».

С такими задачами в наше время приходится иметь дело представителям самых разных специальностей:

• Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;
• Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей;
• Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.

При изучении любой темы у учеников возникает вопрос: «Зачем нам это надо?» Если ответ удовлетворит любопытство, то можно говорить о заинтересованности учеников. Ответ для темы «Производная» можно получить, зная, где используются производные функций.

Чтобы ответить на этот вопрос, можно перечислить некоторые дисциплины и их разделы, в которых применяются производные.

Производная в алгебре:

1. Касательная к графику функции

Касательная к графику функции f, дифференцируемой в точке x о , - это прямая, проходящая через точку (x о ; f (x о )) и имеющая угловой коэффициент f ′(x о ).

Y = f (x о ) + f ′(x о ) (x – x о )

2. Поиск промежутков возрастания и убывания функции

Функция y=f(x) возрастает на интервале X , если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Функция y=f(x) убывает на интервале X , если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.

3. Поиск точек экстремума функции

Точку называют точкой максимума функции y=f(x) , если для всех x . Значение функции в точке максимума называют максимумом функции и обозначают .

Точку называют точкой минимума функции y=f(x) , если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают .

Под окрестностью точки понимают интервал , где - достаточно малое положительное число.

Точки минимума и максимума называют точками экстремума , а значения функции, соответствующие точкам экстремума, называют экстремумами функции .

4. Поиск промежутков выпуклости и вогнутости функции

График функции , является на этом интервале выпуклым , лежит не выше любой своей касательной (рис. 1).

График функции , дифференцируемой на интервале , является на этом интервале вогнутым , если график этой функции в пределах интервала лежит не ниже любой своей касательной (рис. 2).

Точкой перегиба графика функции называется точка , разделяющая промежутки выпуклости и вогнутости.

5. Поиск точек изгиба функции

Производная в физике:

1. Скорость как производная пути

2. Ускорение как производная скорости a =

3. Скорость распада радиоактивных элементов = - λN

А так же в физике производную применяют для вычисления:

Скорости материальной точки

Мгновенной скорости как физический смысл производной

Мгновенное значение силы переменного тока

Мгновенное значение ЭДС электромагнитной индукции

Максимальную мощность

Производная в химии:

И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.

Производную в химии используют для определения очень важной вещи – скорости химической реакции, одного из решающих факторов, который нужно учитывать во многих областях научно-производственной деятельности. V (t) = p ‘(t)

Производная в биологии:

Популяция – это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.

Р = х‘ (t)

Производная в географии:

1. Некоторые значения в сейсмографии

2. Особенности электромагнитного поля земли

3. Радиоактивность ядерно- геоифзичексих показателей

4.Многие значения в экономической географии

5.Вывести формулу для вычисления численности населения на территории в момент времени t.

у’= к у

Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N(t) .Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует

Производная в электротехнике:

В наших домах, на транспорте, на заводах: всюду работает электрический ток. Под электрическим током понимают направленное движение свободных электрически заряженных частиц.

Количественной характеристикой электрического тока является сила тока.

В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.

В электротехнике в основном используется работа переменного тока.

Электрический ток, изменяющийся со временем, называют переменным. Цепь переменного тока может содержать различные элементы: нагревательные приборы, катушки, конденсаторы.

Получение переменного электрического тока основано на законе электромагнитной индукции, формулировка которого содержит производную магнитного потока.

Производная в экономике:

Экономика – основа жизни, а в ней важное место занимает дифференциальное исчисление – аппарат для экономического анализа. Базовая задача экономического анализа – изучение связей экономических величин в виде функций.

Производная в экономике решает важные вопросы:

1. В каком направлении изменится доход государства при увеличении налогов или при введении таможенных пошлин?

2. Увеличится или уменьшится выручка фирмы при увеличение цены на её продукцию?

Для решения этих вопросов нужно построить функции связи входящих переменных, которые затем изучаются методами дифференциального исчисления.

Также с помощью экстремума функции (производной) в экономике можно найти наивысшую производительность труда, максимальную прибыль, максимальный выпуск и минимальные издержки.

ВЫВОД: производная успешно применяется при решении различных прикладных задач в науке, технике и жизни

Как видно из вышеперечисленного применение производной функции весьма многообразно и не только при изучении математики, но и других дисциплин. Поэтому можно сделать вывод, что изучение темы: «Производная функции» будет иметь своё применение в других темах и предметах.

Мы убедились в важности изучения темы "Производная", ее роли в исследовании процессов науки и техники, в возможности конструирования по реальным событиям математические модели, и решать важные задачи.

“Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей”.

Так сказал американский математик Морис Клайн.

Список используемой литературы:

1. Богомолов Н.В., Самойленко И.И. Математика. - М.: Юрайт, 2015.

2. Григорьев В.П., Дубинский Ю.А, Элементы высшей математики. - М.: Академия, 2014.

3. Баврин И.И. Основы высшей математики. - М.: Высшая школа, 2013.

4. Богомолов Н.В. Практические занятия по математике. - М.: Высшая школа, 2013.

5. Богомолов Н.В. Сборник задач по математике. - М.: Дрофа, 2013.

6. Рыбников К.А. История математики, «Издательство Московского университета», М, 1960.

7. Виноградов Ю.Н., Гомола А.И., Потапов В.И., Соколова Е.В. – М.: Издательский центр «Академия», 2010

8. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия. – М.: Издательский центр «Академия», 2016

Периодические источники:

Газеты и журналы: «Математика», «Открытый урок»

Использование ресурсов сети Интернет, электронных библиотек:

www:egetutor.ru

matematika-na5.norod.ru