Решение уравнений высших степеней различными методами. Уравнения высших степеней по математике Решение уравнений с большими степенями

Рассмотрим решения уравнений с одной переменной степени выше второй.

Степенью уравнения Р(х) = 0 называется степень многочлена Р(х), т.е. наибольшая из степеней его членов с коэффициентом, не равным нулю.

Так, например, уравнение (х 3 – 1) 2 + х 5 = х 6 – 2 имеет пятую степень, т.к. после операций раскрытия скобок и приведения подобных получим равносильное уравнение х 5 – 2х 3 + 3 = 0 пятой степени.

Вспомним правила, которые понадобятся для решения уравнений степени выше второй.

Утверждения о корнях многочлена и его делителях:

1. Многочлен n-й степени имеет число корней не превышающее число n, причем корни кратности m встречаются ровно m раз.

2. Многочлен нечетной степени имеет хотя бы один действительный корень.

3. Если α – корень Р(х), то Р n (х) = (х – α) · Q n – 1 (x), где Q n – 1 (x) – многочлен степени (n – 1).

4.

5. Приведенный многочлен с целыми коэффициентами не может иметь дробных рациональных корней.

6. Для многочлена третьей степени

Р 3 (х) = ах 3 + bx 2 + cx + d возможно одно из двух: либо он разлагается в произведение трех двучленов

Р 3 (x) = а(х – α)(х – β)(х – γ), либо разлагается в произведение двучлена и квадратного трехчлена Р 3 (x) = а(х – α)(х 2 + βх + γ).

7. Любой многочлен четвертой степени раскладывается в произведение двух квадратных трехчленов.

8. Многочлен f(x) делится на многочлен g(х) без остатка, если существует многочлен q(x), что f(x) = g(x) · q(x). Для деления многочленов применяется правило «деления уголком».

9. Для делимости многочлена P(x) на двучлен (x – c) необходимо и достаточно, чтобы число с было корнем P(x) (Следствие теоремы Безу).

10. Теорема Виета: Если х 1 , х 2 , …, х n – действительные корни многочлена

Р(х) = а 0 х n + а 1 х n - 1 + … + а n , то имеют место следующие равенства:

х 1 + х 2 + … + х n = -а 1 /а 0 ,

х 1 · х 2 + х 1 · х 3 + … + х n – 1 · х n = a 2 /а 0 ,

х 1 · х 2 · х 3 + … + х n – 2 · х n – 1 · х n = -a 3 / а 0 ,

х 1 · х 2 · х 3 · х n = (-1) n a n / а 0 .

Решение примеров

Пример 1.

Найти остаток от деления Р(х) = х 3 + 2/3 x 2 – 1/9 на (х – 1/3).

Решение.

По следствию из теоремы Безу: «Остаток от деления многочлена на двучлен (х – с) равен значению многочлена от с». Найдем Р(1/3) = 0. Следовательно, остаток равен 0 и число 1/3 – корень многочлена.

Ответ: R = 0.

Пример 2.

Разделить «уголком» 2х 3 + 3x 2 – 2х + 3 на (х + 2). Найти остаток и неполное частное.

Решение:

2х 3 + 3x 2 – 2х + 3| х + 2

2х 3 + 4 x 2 2x 2 – x

X 2 – 2 x

Ответ: R = 3; частное: 2х 2 – х.

Основные методы решения уравнений высших степеней

1. Введение новой переменной

Метод введения новой переменной уже знаком на примере биквадратных уравнений. Он заключается в том, что для решения уравнения f(x) = 0 вводят новую переменную (подстановку) t = x n или t = g(х) и выражают f(x) через t, получая новое уравнение r(t). Решая затем уравнение r(t), находят корни:

(t 1 , t 2 , …, t n). После этого получают совокупность n уравнений q(x) = t 1 , q(x) = t 2 , … , q(x) = t n , из которых находят корни исходного уравнения.

Пример 1.

(х 2 + х + 1) 2 – 3х 2 – 3x – 1 = 0.

Решение:

(х 2 + х + 1) 2 – 3(х 2 + x) – 1 = 0.

(х 2 + х + 1) 2 – 3(х 2 + x + 1) + 3 – 1 = 0.

Замена (х 2 + х + 1) = t.

t 2 – 3t + 2 = 0.

t 1 = 2, t 2 = 1. Обратная замена:

х 2 + х + 1 = 2 или х 2 + х + 1 = 1;

х 2 + х - 1 = 0 или х 2 + х = 0;

Ответ: Из первого уравнения: х 1, 2 = (-1 ± √5)/2, из второго: 0 и -1.

2. Разложение на множители методом группировки и формул сокращенного умножения

Основа данного метода также не нова и заключается в группировке слагаемых таким образом, чтобы каждая группа содержала общий множитель. Для этого иногда приходится применять некоторые искусственные приемы.

Пример 1.

х 4 – 3x 2 + 4х – 3 = 0.

Решение.

Представим - 3x 2 = -2x 2 – x 2 и сгруппируем:

(х 4 – 2x 2) – (x 2 – 4х + 3) = 0.

(х 4 – 2x 2 +1 – 1) – (x 2 – 4х + 3 + 1 – 1) = 0.

(х 2 – 1) 2 – 1 – (x – 2) 2 + 1 = 0.

(х 2 – 1) 2 – (x – 2) 2 = 0.

(х 2 – 1 – х + 2)(х 2 – 1 + х - 2) = 0.

(х 2 – х + 1)(х 2 + х – 3) = 0.

х 2 – х + 1 = 0 или х 2 + х – 3 = 0.

Ответ: В первом уравнении нет корней, из второго: х 1, 2 = (-1 ± √13)/2.

3. Разложение на множитель методом неопределенных коэффициентов

Суть метода состоит в том, что исходный многочлен раскладывается на множители с неизвестными коэффициентами. Используя свойство, что многочлены равны, если равны их коэффициенты при одинаковых степенях, находят неизвестные коэффициенты разложения.

Пример 1.

х 3 + 4x 2 + 5х + 2 = 0.

Решение.

Многочлен 3-й степени можно разложить в произведение линейного и квадратного множителей.

х 3 + 4x 2 + 5х + 2 = (х – а)(x 2 + bх + c),

х 3 + 4x 2 + 5х + 2 = х 3 +bx 2 + cх – ax 2 – abх – ac,

х 3 + 4x 2 + 5х + 2 = х 3 + (b – a)x 2 + (cх – ab)х – ac.

Решив систему:

{b – a = 4,
{c – ab = 5,
{-ac = 2,

{a = -1,
{b = 3,
{c = 2, т.е.

х 3 + 4x 2 + 5х + 2 = (х + 1)(x 2 + 3х + 2).

Корни уравнения (х + 1)(x 2 + 3х + 2) = 0 находятся легко.

Ответ: -1; -2.

4. Метод подбора корня по старшему и свободному коэффициенту

Метод опирается на применение теорем:

1) Всякий целый корень многочлена с целыми коэффициентами является делителем свободного члена.

2) Для того, чтобы несократимая дробь p/q (p – целое, q – натуральное) была корнем уравнения с целыми коэффициентами, необходимо, чтобы число p было целым делителем свободного члена а 0 , а q – натуральным делителем старшего коэффициента.

Пример 1.

6х 3 + 7x 2 – 9х + 2 = 0.

Решение:

6: q = 1, 2, 3, 6.

Следовательно, p/q = ±1, ±2, ±1/2, ±1/3, ±2/3, ±1/6.

Найдя один корень, например – 2, другие корни найдем, используя деление уголком, метод неопределенных коэффициентов или схему Горнера.

Ответ: -2; 1/2; 1/3.

Остались вопросы? Не знаете, как решать уравнения?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

В общем случае уравнение, имеющее степень выше 4 , нельзя разрешить в радикалах. Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4 -х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи.

Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попробовать найти рациональные корни, а потом разложить многочлен на множители, чтобы потом преобразовать его в уравнение более низкой степени, которое будет просто решить. В рамках этого материала мы рассмотрим как раз такие примеры.

Уравнения высшей степени с целыми коэффициентами

Все уравнения, имеющие вид a n x n + a n - 1 x n - 1 + . . . + a 1 x + a 0 = 0 , мы можем привести к уравнению той же степени с помощью умножения обеих частей на a n n - 1 и осуществив замену переменной вида y = a n x:

a n x n + a n - 1 x n - 1 + . . . + a 1 x + a 0 = 0 a n n · x n + a n - 1 · a n n - 1 · x n - 1 + … + a 1 · (a n) n - 1 · x + a 0 · (a n) n - 1 = 0 y = a n x ⇒ y n + b n - 1 y n - 1 + … + b 1 y + b 0 = 0

Те коэффициенты, что получились в итоге, также будут целыми. Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид x n + a n x n - 1 + … + a 1 x + a 0 = 0 .

Вычисляем целые корни уравнения. Если уравнение имеет целые корни, нужно искать их среди делителей свободного члена a 0 . Выпишем их и будем подставлять в исходное равенство по очереди, проверяя результат. Как только мы получили тождество и нашли один из корней уравнения, то можем записать его в виде x - x 1 · P n - 1 (x) = 0 . Здесь x 1 является корнем уравнения, а P n - 1 (x) представляет собой частное от деления x n + a n x n - 1 + … + a 1 x + a 0 на x - x 1 .

Подставляем остальные выписанные делители в P n - 1 (x) = 0 , начав с x 1 , поскольку корни могут повторяться. После получения тождества корень x 2 считается найденным, а уравнение может быть записано в виде (x - x 1) (x - x 2) · P n - 2 (x) = 0 .Здесь P n - 2 (x) будет частным от деления P n - 1 (x) на x - x 2 .

Продолжаем и дальше перебирать делители. Найдем все целые корни и обозначим их количество как m . После этого исходное уравнение можно представить как x - x 1 x - x 2 · … · x - x m · P n - m (x) = 0 . Здесь P n - m (x) является многочленом n - m -ной степени. Для подсчета удобно использовать схему Горнера.

Если у нас исходное уравнение имеет целые коэффициенты, мы не можем получить в итоге дробные корни.

У нас в итоге получилось уравнение P n - m (x) = 0 , корни которого могут быть найдены любым удобным способом. Они могут быть иррациональными или комплексными.

Покажем на конкретном примере, как применяется такая схема решения.

Пример 1

Условие: найдите решение уравнения x 4 + x 3 + 2 x 2 - x - 3 = 0 .

Решение

Начнем с нахождений целых корней.

У нас есть свободный член, равный минус трем. У него есть делители, равные 1 , - 1 , 3 и - 3 . Подставим их в исходное уравнение и посмотрим, какие из них дадут в итоге тождества.

При x , равном единице, мы получим 1 4 + 1 3 + 2 · 1 2 - 1 - 3 = 0 , значит, единица будет корнем данного уравнения.

Теперь выполним деления многочлена x 4 + x 3 + 2 x 2 - x - 3 на (х - 1) в столбик:

Значит, x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3 .

1 3 + 2 · 1 2 + 4 · 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 · (- 1) 2 + 4 · - 1 + 3 = 0

У нас получилось тождество, значит, мы нашли еще один корень уравнения, равный - 1 .

Делим многочлен x 3 + 2 x 2 + 4 x + 3 на (х + 1) в столбик:

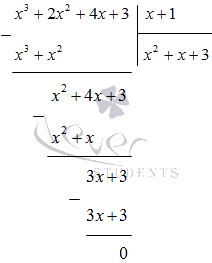
Получаем, что

x 4 + x 3 + 2 x 2 - x - 3 = (x - 1) (x 3 + 2 x 2 + 4 x + 3) = = (x - 1) (x + 1) (x 2 + x + 3)

Подставляем очередной делитель в равенство x 2 + x + 3 = 0 , начиная с - 1:

1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0

Равенства, полученные в итоге, будут неверными, значит, у уравнения больше нет целых корней.

Оставшиеся корни будут корнями выражения x 2 + x + 3 .

D = 1 2 - 4 · 1 · 3 = - 11 < 0

Из этого следует, что у данного квадратного трехчлена нет действительных корней, но есть комплексно сопряженные: x = - 1 2 ± i 11 2 .

Уточним, что вместо деления в столбик можно применять схему Горнера. Это делается так: после того, как мы определили первый корень уравнения, заполняем таблицу.

В таблице коэффициентов мы сразу можем увидеть коэффициенты частного от деления многочленов, значит, x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3 .

После нахождения следующего корня, равного - 1 , мы получаем следующее:

Ответ: х = - 1 , х = 1 , x = - 1 2 ± i 11 2 .

Пример 2

Условие: решите уравнение x 4 - x 3 - 5 x 2 + 12 = 0 .

Решение

У свободного члена есть делители 1 , - 1 , 2 , - 2 , 3 , - 3 , 4 , - 4 , 6 , - 6 , 12 , - 12 .

Проверяем их по порядку:

1 4 - 1 3 - 5 · 1 2 + 12 = 7 ≠ 0 (- 1) 4 - (- 1) 3 - 5 · (- 1) 2 + 12 = 9 ≠ 0 2 4 · 2 3 - 5 · 2 2 + 12 = 0

Значит, x = 2 будет корнем уравнения. Разделим x 4 - x 3 - 5 x 2 + 12 на х - 2 , воспользовавшись схемой Горнера:

В итоге мы получим x - 2 (x 3 + x 2 - 3 x - 6) = 0 .

2 3 + 2 2 - 3 · 2 - 6 = 0

Значит, 2 опять будет корнем. Разделим x 3 + x 2 - 3 x - 6 = 0 на x - 2:

В итоге получим (x - 2) 2 · (x 2 + 3 x + 3) = 0 .

Проверка оставшихся делителей смысла не имеет, поскольку равенство x 2 + 3 x + 3 = 0 быстрее и удобнее решить с помощью дискриминанта.

Решим квадратное уравнение:

x 2 + 3 x + 3 = 0 D = 3 2 - 4 · 1 · 3 = - 3 < 0

Получаем комплексно сопряженную пару корней: x = - 3 2 ± i 3 2 .

Ответ : x = - 3 2 ± i 3 2 .

Пример 3

Условие: найдите для уравнения x 4 + 1 2 x 3 - 5 2 x - 3 = 0 действительные корни.

Решение

x 4 + 1 2 x 3 - 5 2 x - 3 = 0 2 x 4 + x 3 - 5 x - 6 = 0

Выполняем домножение 2 3 обеих частей уравнения:

2 x 4 + x 3 - 5 x - 6 = 0 2 4 · x 4 + 2 3 x 3 - 20 · 2 · x - 48 = 0

Заменяем переменные y = 2 x:

2 4 · x 4 + 2 3 x 3 - 20 · 2 · x - 48 = 0 y 4 + y 3 - 20 y - 48 = 0

В итоге у нас получилось стандартное уравнение 4 -й степени, которое можно решить по стандартной схеме. Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y = - 2 , y = 3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x = y 2 = - 2 2 = - 1 и x = y 2 = 3 2 .

Ответ: x 1 = - 1 , x 2 = 3 2

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Уравнения высших степеней (корни многочлена от одной переменной).

П лан лекции. № 1 . Уравнения высших степеней в школьном курсе математики. № 2 . Стандартный вид многочлена. № 3 .Целые корни многочлена. Схема Горнера. № 4. Дробные корни многочлена. № 5. Уравнения вида: (х + а)(х + в)(х + с) … = А № 6. Возвратные уравнения. № 7. Однородные уравнения. № 8. Метод неопределенных коэффициентов. № 9. Функционально – графический метод. № 10. Формулы Виета для уравнений высших степеней. № 11. Нестандартные методы решения уравнений высших степеней.

Уравнения высших степеней в школьном курсе математики. 7 класс. Стандартный вид многочлена. Действия с многочленами. Разложение многочлена на множители. В обычном классе 42 часа, в спец классе 56 часов. 8 спецкласс. Целые корни многочлена, деление многочленов, возвратные уравнения, разность и сумма п – ых степеней двучлена, метод неопределенных коэффициентов. Ю.Н. Макарычев « Дополнительные главы к школьному курсу алгебры 8 класса», М.Л.Галицкий Сборник задач по алгебре 8 – 9 класс». 9 спецкласс. Рациональные корни многочлена. Обобщенные возвратные уравнения. Формулы Виета для уравнений высших степеней. Н.Я. Виленкин « Алгебра 9 класс с углубленным изучением. 11 спецкласс. Тождественность многочленов. Многочлен от нескольких переменных. Функционально – графический метод решения уравнений высших степеней.

Стандартный вид многочлена. Многочлен Р(х) = а ⁿ х ⁿ + а п-1 х п-1 + … + а₂х ² + а₁х + а₀. Называется многочленом стандартного вида. а п х ⁿ - старший член многочлена а п - коэффициент при старшем члене многочлена. При а п = 1 Р(х) называется приведенным многочленом. а ₀ - свободный член многочлена Р(х). п – степень многочлена.

Целые корни многочлена. Схема Горнера. Теорема № 1. Если целое число а является корнем многочлена Р(х), то а – делитель свободного члена Р(х). Пример № 1 . Решите уравнение. Х⁴ + 2х³ = 11х² – 4х – 4 Приведем уравнение к стандартному виду. Х⁴ + 2х³ - 11х² + 4х + 4 = 0. Имеем многочлен Р(х) = х ⁴ + 2х³ - 11х² + 4х + 4 Делители свободного члена: ± 1, ± 2, ±4. х = 1 корень уравнения т.к. Р(1) = 0, х = 2 корень уравнения т.к. Р(2) = 0 Теорема Безу. Остаток от деления многочлена Р(х) на двучлен (х – а) равен Р(а). Следствие. Если а – корень многочлена Р(х), то Р(х) делится на (х – а). В нашем уравнении Р(х) делится на (х – 1) и на (х – 2), а значит и на (х – 1) (х – 2). При делении Р(х) на (х ² - 3х + 2) в частном получается трехчлен х ² + 5х + 2 = 0, который имеет корни х =(-5 ± √17)/2

Дробные корни многочлена. Теорема №2. Если р / g корень многочлена Р(х), то р – делитель свободного члена, g – делитель коэффициента старшего члена Р(х). Пример № 2. Решите уравнение. 6х³ - 11х² - 2х + 8 = 0. Делители свободного члена: ±1, ±2, ±4, ±8. Ни одно из этих чисел не удовлетворяет уравнению. Целых корней нет. Натуральные делители коэффициента старшего члена Р(х): 1, 2, 3, 6. Возможные дробные корни уравнения: ±2/3, ±4/3, ±8/3. Проверкой убеждаемся, что Р(4/3) = 0. Х = 4/3 корень уравнения. По схеме Горнера разделим Р(х) на (х – 4/3).

Примеры для самостоятельного решения. Решите уравнения: 9х³ - 18х = х – 2, х ³ - х ² = х – 1, х ³ - 3х² -3х + 1 = 0, Х ⁴ - 2х³ + 2х – 1 = 0, Х⁴ - 3х² + 2 = 0, х ⁵ + 5х³ - 6х² = 0, х ³ + 4х² + 5х + 2 = 0, Х⁴ + 4х³ - х ² - 16х – 12 = 0 4х³ + х ² - х + 5 = 0 3х⁴ + 5х³ - 9х² - 9х + 10 = 0. Ответы: 1) ±1/3; 2 2) ±1, 3) -1; 2 ±√3 , 4) ±1, 5) ± 1; ±√2 , 6) 0; 1 7) -2; -1, 8) -3; -1; ±2, 9) – 5/4 10) -2; - 5/3; 1.

Уравнения вида (х + а)(х + в)(х + с)(х + d)… = А. Пример №3 . Решите уравнение (х + 1)(х + 2)(х + 3)(х + 4) =24. а = 1, в = 2, с = 3, d = 4 а + d = в + с. Перемножаем первую скобку с четвертой и вторую с третьей. (х + 1)(х + 4)(х + 20(х + 3) = 24. (х ² + 5х + 4)(х ² + 5х + 6) = 24. Пусть х ² + 5х + 4 = у, тогда у(у + 2) = 24, у² + 2у – 24 = 0 у₁ = - 6, у₂ = 4. х ² + 5х + 4 = -6 или х ² + 5х + 4 = 4. х ² + 5х + 10 = 0, Д

Примеры для самостоятельного решения. (х + 1)(х + 3)(х + 5)(х + 7) = -15, х (х + 4)(х + 5)(х + 9) + 96 = 0, х (х + 3)(х + 5)(х + 8) + 56 = 0, (х – 4)(х – 3)(х – 2)(х – 1) = 24, (х – 3)(х -4)(х – 5)(х – 6) = 1680, (х ² - 5х)(х + 3)(х – 8) + 108 = 0, (х + 4)² (х + 10)(х – 2) + 243 = 0 (х ² + 3х + 2)(х ² + 9х + 20) = 4, Указание: х + 3х + 2 = (х + 1)(х + 2), х ² + 9х + 20 = (х + 4)(х + 5) Ответы: 1) -4 ±√6; - 6; - 2. 6) - 1; 6; (5± √97)/2 7) -7; -1; -4 ±√3.

Возвратные уравнения. Определение №1. Уравнение вида: ах⁴ + вх ³ + сх ² + вх + а = 0 называется возвратным уравнением четвертой степени. Определение №2. Уравнение вида: ах⁴ + вх ³ + сх ² + квх + к² а = 0 называется обобщенным возвратным уравнением четвертой степени. к² а: а = к² ; кв: в = к. Пример №6. Решите уравнение х ⁴ - 7х³ + 14х² - 7х + 1 = 0. Делим обе части уравнения на х ² . х ² - 7х + 14 – 7/ х + 1/ х ² = 0, (х ² + 1/ х ²) – 7(х + 1/ х) + 14 = 0. Пусть х + 1/ х = у. Возводим обе части равенства в квадрат. х ² + 2 + 1/ х ² = у² , х ² + 1/ х ² = у² - 2. Получаем квадратное уравнение у² - 7у + 12 = 0, у₁ = 3, у₂ = 4. х + 1/ х =3 или х + 1/ х = 4. Получаем два уравнения: х ² - 3х + 1 = 0, х ² - 4х + 1 = 0. Пример №7. 3х⁴ - 2х³ - 31х² + 10х + 75 = 0. 75:3 = 25, 10:(– 2) = -5, (-5)² = 25. Условие обобщенного возвратного уравнения выполняется к= -5. Решается аналогично примеру №6. Делим обе части уравнения на х ². 3х⁴ - 2х – 31 + 10/ х + 75/ х ² = 0, 3(х ⁴ + 25/ х ²) – 2(х – 5/ х) – 31 = 0. Пусть х – 5/ х = у, возводим обе части равенства в квадрат х ² - 10 + 25/ х ² = у² , х ² + 25/ х ² = у² + 10. Имеем квадратное уравнение 3у² - 2у – 1 = 0, у₁ = 1, у₂ = - 1/3. х – 5/ х = 1 или х – 5/ х = -1/3. Получаем два уравнения: х ² - х – 5 = 0 и 3х² + х – 15 = 0

Примеры для самостоятельного решения. 1. 78х⁴ - 133х³ + 78х² - 133х + 78 = 0, 2. х ⁴ - 5х³ + 10х² - 10х + 4 = 0, 3. х ⁴ - х ³ - 10х² + 2х + 4 = 0, 4. 6х⁴ + 5х³ - 38х² -10х + 24 = 0, 5. х ⁴ + 2х³ - 11х² + 4х + 4 = 0, 6. х ⁴ - 5х³ + 10х² -10х + 4 = 0. Ответы: 1) 2/3; 3/2, 2) 1;2 3) -1 ±√3; (3±√17)/2, 4) -1±√3; (7±√337)/12 5) 1; 2; (-5± √17)/2, 6) 1; 2.

Однородные уравнения. Определение. Уравнение вида а₀ u³ + а₁ u² v + а₂ uv² + а₃ v³ = 0 называется однородным уравнением третьей степени относительно u v . Определение. Уравнение вида а₀ u⁴ + а₁ u³v + а₂ u²v² + а₃ uv³ + а₄ v⁴ = 0 называется однородным уравнением четвертой степени относительно u v . Пример №8. Решите уравнение (х ² - х + 1)³ + 2х⁴(х ² - х + 1) – 3х⁶ = 0 Однородное уравнение третьей степени относительно u = х ²- х + 1, v = х ². Делим обе части уравнения на х ⁶. Предварительно проверили, что х = 0 не является корнем уравнения. (х ² - х + 1/ х ²)³ + 2(х ² - х + 1/ х ²) – 3 = 0. (х ² - х + 1)/ х ²) = у, у³ + 2у – 3 = 0, у = 1 корень уравнения. Делим многочлен Р(х) = у³ + 2у – 3 на у – 1 по схеме Горнера. В частном получаем трехчлен, который не имеет корней. Ответ: 1.

Примеры для самостоятельного решения. 1. 2(х ² + 6х + 1)² + 5(Х² + 6Х + 1)(Х² + 1) + 2(Х² + 1)² = 0, 2. (Х + 5)⁴ - 13Х²(Х + 5)² + 36Х⁴ = 0, 3. 2(Х² + Х + 1)² - 7(Х – 1)² = 13(Х³ - 1), 4. 2(Х -1)⁴ - 5(Х² - 3Х + 2)² + 2(х – 2)⁴ = 0, 5. (х ² + х + 4)² + 3х(х ² + х + 4) + 2х² = 0, Ответы: 1) -1; -2±√3, 2) -5/3; -5/4; 5/2; 5 3) -1; -1/2; 2;4 4) ±√2; 3±√2, 5) Корней нет.

Метод неопределенных коэффициентов. Теорема №3. Два многочлена Р(х) и G(х) тождественны тогда и только тогда, когда они имеют одинаковую степень и коэффициенты при одноименных степенях переменной в обоих многочленах равны. Пример №9. Разложить на множители многочлен у⁴ - 4у³ + 5у² - 4у + 1. у⁴ - 4у³ + 5у² - 4у + 1 = (у² + ву + с)(у² + в₁у + с₁) =у ⁴ +у³(в₁ + в) + у²(с₁ + с + в₁в) + у(вс ₁ + св ₁) + сс ₁. Согласно теореме №3 имеем систему уравнений: в₁ + в = -4, с₁ + с + в₁в = 5, вс ₁ + св ₁ = -4, сс ₁ = 1. Необходимо решить систему в целых числах. Последнее уравнение в целых числах может иметь решения: с = 1, с₁ =1; с = -1, с₁ = -1. Пусть с = с ₁ = 1, тогда из первого уравнения имеем в₁ = -4 –в. Подставляем во второе уравнение системы в² + 4в + 3 = 0, в = -1, в₁ = -3 или в = -3, в₁ = -1. Данные значения подходят третьему уравнению системы. При с = с ₁ = -1 Д

Пример №10. Разложить на множители многочлен у³ - 5у + 2. у³ -5у + 2 = (у + а)(у² + ву + с) = у³ + (а + в)у² + (ав +с)у + ас. Имеем систему уравнений: а + в = 0, ав + с = -5, ас = 2. Возможные целые решения третьего уравнения: (2; 1), (1; 2), (-2; -1), (-1; -2). Пусть а = -2, с = -1. Из первого уравнения системы в = 2, что удовлетворяет второму уравнению. Подставляя данные значения в искомое равенство получим ответ: (у – 2)(у² + 2у – 1). Второй способ. У³ - 5у + 2 = у³ -5у + 10 – 8 = (у³ - 8) – 5(у – 2) = (у – 2)(у² + 2у -1).

Примеры для самостоятельного решения. Разложите на множители многочлены: 1. у⁴ + 4у³ + 6у² +4у -8, 2. у⁴ - 4у³ + 7у² - 6у + 2, 3. х ⁴ + 324, 4. у⁴ -8у³ + 24у² -32у + 15, 5. Решите уравнение, используя метод разложения на множители: а) х ⁴ -3х² + 2 = 0, б) х ⁵ +5х³ -6х² = 0. Ответы: 1) (у² +2у -2)(у² +2у +4), 2) (у – 1)²(у² -2у + 2), 3) (х ² -6х + 18)(х ² + 6х + 18), 4) (у – 1)(у – 3)(у² -4у + 5), 5а) ± 1; ±√2 , 5б) 0; 1.

Функционально – графический метод решения уравнений высших степеней. Пример №11. Решите уравнение х ⁵ + 5х -42 = 0. Функция у = х ⁵ возрастающая, функция у = 42 – 5х убывающая (к

Примеры для самостоятельного решения. 1. Используя свойство монотонности функции, докажите, что уравнение имеет единственный корень, и найдите этот корень: а) х ³ = 10 – х, б) х ⁵ + 3х³ - 11√2 – х. Ответы: а) 2, б) √2. 2. Решите уравнение, используя функционально – графический метод: а) х = ³ √х, б) l х l = ⁵ √х, в) 2 = 6 – х, г) (1/3) = х +4, д) (х – 1)² = log₂ х, е) log = (х + ½)² , ж) 1 - √х = ln х, з) √х – 2 = 9/х. Ответы: а) 0; ±1, б) 0; 1, в) 2, г) -1, д) 1; 2, е) ½, ж) 1, з) 9.

Формулы Виета для уравнений высших степеней. Теорема №5 (Теореме Виета). Если уравнение а х ⁿ + а х ⁿ + … + а₁х + а₀ имеет n различных действительных корней х ₁, х ₂, … , х, то они удовлетворяют равенствам: Для квадратного уравнения ах² + вх + с = о: х ₁ + х ₂ = -в/а, х₁х ₂ = с/а; Для кубического уравнения а₃х ³ + а₂х ² + а₁х + а₀ = о: х ₁ + х ₂ + х ₃ = -а₂/а₃; х₁х ₂ + х₁х ₃ + х₂х ₃ = а₁/а₃; х₁х₂х ₃ = -а₀/а₃; …, для уравнения n –ой степени: х ₁ + х ₂ + … х = - а / а, х₁х ₂ + х₁х ₃ + … + х х = а / а, … , х₁х ₂·… · х = (- 1) ⁿ а₀/а. Выполняется и обратная теорема.

Пример №13. Напишите кубическое уравнение, корни которого обратны корням уравнения х ³ - 6х² + 12х – 18 = 0, а коэффициент при х ³ равен 2. 1. По теореме Виета для кубического уравнения имеем: х ₁ + х ₂ + х ₃ = 6, х₁х ₂ + х₁х ₃ + х₂х ₃ = 12, х₁х₂х ₃ = 18. 2. Составляем обратные величины данным корням и для них применяем обратную теорему Виета. 1/ х ₁ + 1/ х ₂ + 1/ х ₃ = (х₂х ₃ + х₁х ₃ + х₁х ₂)/ х₁х₂х ₃ = 12/18 = 2/3. 1/ х₁х ₂ + 1/ х₁х ₃ + 1/ х₂х ₃ = (х ₃ + х ₂ + х ₁)/ х₁х₂х ₃ = 6/18 = 1/3, 1/ х₁х₂х ₃ = 1/18. Получаем уравнение х ³ +2/3х² + 1/3х – 1/18 = 0 · 2 Ответ: 2х³ + 4/3х² + 2/3х -1/9 = 0.

Примеры для самостоятельного решения. 1. Напишите кубическое уравнение, корни которого обратны квадратам корней уравнения х ³ - 6х² + 11х – 6 = 0, а коэффициент при х ³ равен 8. Ответ: 8х³ - 98/9х² + 28/9х -2/9 = 0. Нестандартные методы решений уравнений высших степеней. Пример №12. Решите уравнение х ⁴ -8х + 63 = 0. Разложим левую часть уравнения на множители. Выделим точные квадраты. Х⁴ - 8х + 63 = (х ⁴ + 16х² + 64) – (16х² + 8х + 1) = (х ² + 8)² - (4х + 1)² = (х ² + 4х + 9)(х ² - 4х + 7) = 0. Оба дискриминанта отрицательные. Ответ: нет корней.

Пример №14. Решите уравнение 21х³ + х ² - 5х – 1 = 0. Если свободный член уравнения равен ± 1, то уравнение преобразуется в приведенное уравнение с помощью замены х = 1/у. 21/у³ + 1/у² - 5/у – 1 = 0 · у³, у³ + 5у² -у – 21 = 0. у = -3 корень уравнения. (у + 3)(у² + 2у -7) = 0, у = -1 ± 2√2. х ₁ = -1/3, х ₂ = 1/ -1 + 2√2 = (2√2 + 1)/7, Х₃ = 1/-1 -2√2 =(1-2√2)/7. Пример №15. Решите уравнение 4х³-10х² + 14х – 5 = 0. Умножим обе части уравнения на 2. 8х³ -20х² + 28х – 10 = 0, (2х)³ - 5(2х)² + 14·(2х) -10 = 0. Введем новую переменную у = 2х, получим приведенное уравнение у³ - 5у² + 14у -10 = 0, у = 1 корень уравнения. (у – 1)(у² - 4у + 10) = 0, Д

Пример №16. Доказать, что уравнение х ⁴ + х ³ + х – 2 = 0 имеет один положительный корень. Пусть f (х) = х ⁴ + х ³ + х – 2, f’ (х) = 4х³ + 3х² + 1 > о при х > о. Функция f (х) возрастающая при х > о, а значение f (о) = -2. Очевидно, что уравнение имеет один положительный корень ч.т.д. Пример №17. Решите уравнение 8х(2х² - 1)(8х⁴ - 8х² + 1) = 1. И.Ф.Шарыгин « Факультативный курс по математике для 11 класса».М. Просвещение 1991 стр90. 1. l х l 1 2х² - 1 > 1 и 8х⁴ -8х² + 1 > 1 2. Сделаем замену х = cosy , у € (0; п). При остальных значениях у, значения х повторяются, а уравнение имеет не более 7 корней. 2х² - 1 = 2 cos²y – 1 = cos2y , 8х⁴ - 8х² + 1 = 2(2х² - 1)² - 1 = 2 cos²2y – 1 = cos4y . 3. Уравнение принимает вид 8 cosycos2ycos4y = 1. Умножаем обе части уравнения на siny . 8 sinycosycos2ycos4y = siny . Применяя 3 раза формулу двойного угла получим уравнение sin8y = siny , sin8y – siny = 0

Окончание решения примера №17. Применяем формулу разности синусов. 2 sin7y/2 · cos9y/2 = 0 . Учитывая, что у € (0;п), у = 2пк/3, к = 1, 2, 3 или у = п /9 + 2пк/9, к =0, 1, 2, 3. Возвращаясь к переменной х получаем ответ: Cos2 п /7, cos4 п /7, cos6 п /7, cos п /9, ½, cos5 п /9, cos7 п /9 . Примеры для самостоятельного решения. Найти все значения а, при которых уравнение (х ² + х)(х ² + 5х + 6) = а имеет ровно три корня. Ответ: 9/16. Указание: построить график левой части уравнения. F max = f(0) = 9/16 . Прямая у = 9/16 пересекает график функции в трех точках. Решите уравнение (х ² + 2х)² - (х + 1)² = 55. Ответ: -4; 2. Решите уравнение (х + 3)⁴ + (х + 5)⁴ = 16. Ответ: -5; -3. Решите уравнение 2(х ² + х + 1)² -7(х – 1)² = 13(х ³ - 1).Ответ: -1; -1/2, 2;4 Найдите число действительных корней уравнения х ³ - 12х + 10 = 0 на [-3; 3/2]. Указание: найти производную и исследовать на монот.

Примеры для самостоятельного решения (продолжение). 6. Найдите число действительных корней уравнения х ⁴ - 2х³ + 3/2 = 0. Ответ: 2 7. Пусть х ₁, х ₂, х ₃ - корни многочлена Р(х) = х ³ - 6х² -15х + 1. Найдите Х₁² + х ₂² + х ₃². Ответ: 66. Указание: примените теорему Виета. 8. Докажите, что при а > о и произвольном вещественном в уравнение х ³ + ах + в = о имеет только один вещественный корень. Указание: проведите доказательство от противного. Примените теорему Виета. 9. Решите уравнение 2(х ² + 2)² = 9(х ³ + 1). Ответ: ½; 1; (3 ± √13)/2. Указание: приведите уравнение к однородному, используя равенства Х² + 2 = х + 1 + х ² - х + 1, х ³ + 1 = (х + 1)(х ² - х + 1). 10. Решите систему уравнений х + у = х ², 3у – х = у². Ответ: (0;0),(2;2), (√2; 2 - √2), (- √2 ; 2 + √2). 11. Решите систему: 4у² -3ху = 2х –у, 5х² - 3у² = 4х – 2у. Ответ: (о;о), (1;1),(297/265; - 27/53).

Контрольная работа. 1 вариант. 1. Решите уравнение (х ² + х) – 8(х ² + х) + 12 = 0. 2. Решите уравнение (х + 1)(х + 3)(х + 5)(х + 7) = - 15. 3. Решите уравнение 12х²(х – 3) + 64(х – 3)² = х ⁴. 4. Решите уравнение х ⁴ - 4х³ + 5х² - 4х + 1 = 0 5. Решите систему аравнений: х ² + 2у² - х + 2у = 6, 1,5х² + 3у² - х + 5у = 12.

2 вариант 1. (х ² - 4х)² + 7(х ² - 4х) + 12 = 0. 2. х (х + 1)(х + 5)(х + 6) = 24. 3. х ⁴ + 18(х + 4)² = 11х²(х + 4). 4. х ⁴ - 5х³ + 6х² - 5х + 1 = 0. 5. х ² - 2ху + у² + 2х²у – 9 = 0, х – у – х²у + 3 = 0. 3 вариант. 1. (х ² + 3х)² - 14(х ² + 3х) + 40 = 0 2. (х – 5)(х-3)(х + 3)(х + 1) = - 35. 3. х4 + 8х²(х + 2) = 9(х+ 2)². 4. х ⁴ - 7х³ + 14х² - 7х + 1 = 0. 5. х + у + х ² + у ² = 18, ху + х ² + у² = 19.

4 вариант. (х ² - 2х)² - 11(х ² - 2х) + 24 = о. (х -7)(х-4)(х-2)(х + 1) = -36. Х⁴ + 3(х -6)² = 4х²(6 – х). Х⁴ - 6х³ + 7х² - 6х + 1 = 0. Х² + 3ху + у² = - 1, 2х² - 3ху – 3у² = - 4. Дополнительное задание: Остаток от деления многочлена Р(х) на (х – 1) равен 4, остаток от делении на (х + 1) равен2, а при делении на (х – 2) равен 8. Найти остаток от деления Р(х) на (х ³ - 2х² - х + 2).

Ответы и указания: вариант № 1 № 2. № 3. № 4. № 5. 1. - 3; ±2; 1 1;2;3. -5; -4; 1; 2. Однородное уравнение: u = x -3, v =x² -2 ; -1; 3; 4. (2;1); (2/3;4/3). Указание: 1·(-3) + 2· 2 2. -6; -2; -4±√6. -3±2√3; - 4; - 2. 1±√11; 4; - 2. Однородное уравнение: u = x + 4, v = x² 1 ; 5;3±√13. (2;1); (0;3); (- 3; 0). Указание: 2· 2 + 1. 3. -6; 2; 4; 12 -3; -2; 4; 12 -6; -3; -1; 2. Однородное u = x+ 2, v = x² -6 ; ±3; 2 (2;3), (3;2), (-2 + √7; -2 - √7); (-2 - √7; -2 + √7). Указание: 2 -1. 4. (3±√5)/2 2±√3 2±√3; (3±√5)/2 (5 ± √21)/2 (1;-2), (-1;2). Указание: 1·4 + 2 .

Решение дополнительного задания. По теореме Безу: Р(1) = 4, Р(-1) = 2, Р(2) = 8. Р(х) = G(x) (х ³ - 2х² - х + 2) + ах² + вх + с. Подставляем 1; - 1; 2. Р(1) = G(1) ·0 + а + в + с = 4, а + в+ с = 4. Р(-1) = а – в + с = 2, Р(2) = 4а² + 2в + с = 8. Решая полученную систему из трех уравнений получим: а = в = 1, с = 2. Ответ: х ² + х + 2.

Критерий № 1 - 2 балла. 1 балл – одна вычислительная ошибка. № 2,3,4 – по 3 балла. 1 балл – привели к квадратному уравнению. 2 балла – одна вычислительная ошибка. № 5. – 4 балла. 1 балл – выразили одну переменную через другую. 2 балла – получили одно из решений. 3 балла – одна вычислительная ошибка. Дополнительное задание: 4 балла. 1 балл – применили теорему Безу для всех четырех случаев. 2 балла – составили систему уравнений. 3 балла – одна вычислительная ошибка.

При решении алгебраических уравнений часто приходится разлагать многочлен на множители. Разложить многочлен на множители – это значит представить его в виде произведения двух или нескольких многочленов. Некоторые методы разложения многочленов мы употребляем достаточно часто: вынесение общего множителя, применение формул сокращенного умножения, выделение полного квадрата, группировка. Рассмотрим ещё некоторые методы.

Иногда при разложении многочлена на множители бывают полезными следующие утверждения:

1) если многочлен, с целыми коэффициентами имеет рациональный корень (где - несократимая дробь,то -делитель свободного члена а делитель старшего коэффициента:

2) Если каким-либо образом подобрать корень многочлена степени, то многочлен можно представить в виде где многочлен степени

Многочлен можно найти либо делением многочлена на двучлен «столбиком», либо соответствующей группировку слагаемых многочлена и выделением из них множителя либо методом неопределенных коэффициентов.

Пример. Разложить на множители многочлен

Решение. Поскольку коэффициент при х4 равен 1, то рациональные корни данного многочлена, существуют, являются делителями числа 6, т. е. могут быть целыми числами ±1, ±2, ±3, ±6. Обозначим данный многочлен через Р4(х). Так как Р Р4 (1) = 4 и Р4(-4) = 23, то числа 1 и -1 не являются корнями многочлена РА{х). Поскольку Р4(2) = 0, то х = 2 является корнем многочлена Р4(х), и, значит, данный многочлен делится на двучлен х - 2. Поэтому х4 -5х3 +7х2 -5х +6 х-2 х4 -2х3 х3 -3х2 +х-3

3х3 +7х2 -5х +6

3х3 +6х2 х2 - 5х + 6 х2- 2х

Следовательно, Р4(х) = (х - 2)(х3 - Зх2 + х - 3). Так как xz - Зх2 + х - 3 = х2 (х - 3) + (х - 3) = (х - 3)(х2 + 1), то х4 - 5х3 + 7х2 - 5х + 6 = (х - 2)(х - 3)(х2 + 1).

Метод введения параметра

Иногда при разложении многочлена на множители помогает метод введения параметра. Суть этого метода поясним на следующем примере.

Пример. х3 –(√3 + 1) х2 + 3.

Решение. Рассмотрим многочлен с параметром а: х3 - (а + 1)х2 + а2, который при а = √3 превращается в заданный многочлен. Запишем этот многочлен как квадратный трехчлен относительно а: аг - ах2 + (х3 - х2).

Так как корни этого квадратного относительно а трехчлена есть а1 = х и а2 = х2 - х, то справедливо равенство а2 - ах2 + {xs - х2) = {а – х)(а - х2 + х). Следовательно, многочлен х3 - (√3 + 1)х2 + 3 разлагается на множители √3 – х и √3 - х2 + х, т. е.

х3 – (√3+1)х2+3=(х-√3)(х2-х-√3).

Метод введения новой неизвестной

В некоторых случаях путем замены выражения f{x), входящего в многочлен Рп{х), через у можно получить многочлен относительно у, который уже легко разложить на множители. Затем после замены у на f{x) получаем разложение на множители многочлена Рп{х).

Пример. Разложить на множители многочлен х(х+1)(х+2)(х+3)-15.

Решение. Преобразуем данный многочлен следующим образом: х(х+1)(х+2)(х+3)-15= [х (х + 3)][(х + 1)(х + 2)] - 15 =(х2 + 3х)(х2 + 3х + 2) - 15.

Обозначим х2 + 3х через у. Тогда имеем у(у + 2) - 15 = у2 + 2у - 15 = у2 + 2у + 1 - 16 = (у + 1)2 - 16 = (у + 1 + 4)(у + 1 - 4)= (у+ 5)(у - 3).

Поэтому х(х + 1)(х+ 2)(х + 3) - 15 = (х2+ 3х + 5)(х2 + 3х - 3).

Пример. Разложить на множители многочлен (х-4)4+(х+2)4

Решение. Обозначим х- 4+х+2 = х - 1 через у.

(х - 4)4 + (х + 2)2= (у - 3)4 + (у + 3)4 = у4 - 12у3 +54у3 - 108у + 81 + у4 + 12у3 + 54у2 + 108у + 81 =

2у4 + 108у2 + 162 = 2(у4 + 54у2 + 81) = 2[(уг + 27)2 - 648] = 2 (у2 + 27 - √б48)(у2 + 27+√б48)=

2((х-1)2+27-√б48)((х-1)2+27+√б48)=2(х2-2х + 28- 18√ 2)(x2- 2x + 28 + 18√ 2).

Комбинирование различных методов

Часто при разложении многочлена на множители приходится применять последовательно несколько из рассмотренных выше методов.

Пример. Разложить на множители многочлен х4 - 3х2 + 4х-3.

Решение. Применяя группировку, перепишем многочлен в виде x4 - 3х2 + 4х - 3 = (х4 – 2х2) – (х2 -4х + 3).

Применяя к первой скобке метод выделения полного квадрата, имеем х4 - 3х3 + 4х - 3 = (х4 - 2 ·1· х2 + 12) - (х2 -4х + 4).

Применяя формулу полного квадрата, можно теперь записать, что х4 – 3х2 + 4x - 3 = (х2 -1)2 - (х - 2)2.

Наконец, применяя формулу разности квадратов, получим, что х4 - 3х2 +4x - 3 = (х2 - 1 + х - 2)(х2 - 1 - х + 2) =(х2+х-3)(х2 -x + 1).

§ 2. Симметрические уравнения

1. Симметрические уравнения третьей степени

Уравнения вида ах3 + bх2 + bх + а = 0, а ≠ 0 (1) называются симметрическими уравнениями третьей степени. Поскольку ах3 + bх2 + bх + а = а(х3 + 1) + bх (х + 1) =(х+1)(ах2+(b-а)х+а), то уравнение (1) равносильно совокупности уравнений х + 1 = 0 и ах2 + (b-а)х + а = 0, решить которую не представляет труда.

Пример 1. Решить уравнение

3х3 + 4х2 + 4х + 3 = 0. (2)

Решение. Уравнение (2) является симметрическим уравнением третьей степени.

Поскольку 3х3 +4хг +4х + 3 = 3(х3 + 1) + 4х(х + 1) = (х+ 1)(3х2 - Зх + 3 + 4х) = (х + 1)(3х2 + х + 3), то уравнение (2) равносильно совокупности уравнений х + 1 = 0 и 3х3 + х +3=0.

Решение первого из этих уравнений есть х = -1, второе уравнение решений не имеет.

Ответ: х = -1.

2. Симметрические уравнения четвертой степени

Уравнение вида

(3) называется симметрическим уравнением четвертой степени.

Поскольку х = 0 не является корнем уравнения(3), то, разделив обе части уравнения(3) на х2, получим уравнение, равносильное исходному(3):

Перепишем уравнение (4) в виде:

В этом уравнение сделаем замену, тогда получим квадратное уравнение

Если уравнение (5) имеет 2 корня у1 и у2, то исходное уравнение равносильно совокупности уравнений

Если же уравнение (5) имеет один корень у0, то исходное уравнение равносильно уравнению

Наконец, если уравнение (5) не имеет корней, то и исходное уравнение также не имеет корней.

Пример 2. Решить уравнение

Решение. Данное уравнение является симметрическим уравнением четвертой степени. Так как х = 0 не является его корнем, то, разделив уравнение (6) на х2, получим равносильное ему уравнение:

Сгруппировав слагаемые, перепишем уравнение (7) в виде или в виде

Положив, получим уравнение имеющее два корня у1 = 2 и у2 = 3. Следовательно, исходное уравнение равносильно совокупности уравнений

Решение первого уравнения этой совокупности есть х1 = 1, а решение второго есть и.

Следовательно, исходное уравнение имеет три корня: х1, х2 и х3.

Ответ: х1=1,.

§3. Алгебраические уравнения

1. Понижение степени уравнения

Некоторые алгебраические уравнения заменой в них некоторого многочлена одной буквой могут быть сведены к алгебраическим уравнениям, степень которых меньше степени исходного уравнения и решение которых проще.

Пример 1. Решить уравнение

Решение. Обозначим через, тогда уравнение (1) можно переписать в виде Последнее уравнение имеет корни и Следовательно, уравнение (1) равносильно совокупности уравнений и. Решение первого уравнения этой совокупности есть и Решения второго уравнения есть

Решениями уравнения (1) являются

Пример 2. Решить уравнение

Решение. Умножив обе части уравнения на 12 и обозначив через,

Получим уравнение Перепишем это уравнение в виде

(3) и обозначив через перепишем уравнение (3) в виде Последнее уравнение имеет корни и Поэтому получаем, что уравнение (3) равносильно совокупности двух уравнений и Решения этой совокупности уравнений есть и т. е. уравнение (2) равносильно совокупности уравнений и (4)

Решениями совокупности (4) является и, они и являются решениями уравнения (2).

2. Уравнения вида

Уравнение

(5) где -данные числа, можно свести к биквадратному уравнению с помощью замены неизвестной т. е. замены

Пример 3. Решить уравнение

Решение. Обозначим через,т. е. сделаем замену переменных или Тогда уравнение (6) можно переписать в виде или, применяя формулу, в виде

Поскольку корни квадратного уравнения есть и то решения уравнения (7) есть решения совокупности уравнений и. Это совокупность уравнений имеет два решения и Следовательно, решения уравнения (6) есть и

3. Уравнения вида

Уравнение

(8) где числа α, β, γ, δ, и Α таковы, что α

Пример 4. Решить уравнение

Решение. Сделаем замену неизвестных т. е. y=x+3 или x = y – 3. Тогда уравнение (9) можно переписать в виде

(y-2)(y-1)(y+1)(y+2)=10, т. е. в виде

(y2- 4)(y2-1)=10(10)

Биквадратное уравнение (10) имеет два корня. Следовательно, уравнение (9) так же имеет два корня:

4. Уравнения вида

Уравнение, (11)

Где, не имеет корня x = 0, поэтому, разделив уравнение (11) на x2 , получим равносильное ему уравнение

Которое после замены неизвестной перепишется в виде квадратного уравнения, решение которого не представляет трудностей.

Пример 5. Решить уравнение

Решение. Так как ч = 0 не является корнем уравнения (12), то, разделив его на x2, получим равносильное ему уравнение

Делая замену неизвестной, получим уравнение (y+1)(y+2)=2, которое имеет два корня: y1 = 0 и y1 = -3. Следовательно, исходное уравнение (12) равносильно совокупности уравнений

Эта совокупность имеет два корня: x1= -1 и x2 = -2.

Ответ: x1= -1, x2 = -2.

Замечание. Уравнение вида,

У которого, всегда можно привести к виду (11) и, более того, считая α > 0 и λ > 0 к виду.

5. Уравнения вида

Уравнение

,(13) где числа, α, β, γ, δ, и Α таковы, что αβ = γδ ≠ 0, можно переписать, перемножив первую скобку со второй, а третью с четвертой, в виде т. е. уравнение (13) теперь записано в виде (11), и его решение можно проводить так же, как и решение уравнения (11).

Пример 6. Решить уравнение

Решение. Уравнение (14) имеет вид (13) , поэтому перепишем его в виде

Так как х = 0 не есть решение этого уравнения, то, разделив его обе части на х2, получим равносильное исходное уравнение. Делая замену переменных, получаем квадратное уравнение, решение которого есть и. Следовательно, исходное уравнение (14) равносильно совокупности уравнений и.

Решение первого уравнения этой совокупности есть

Второе уравнение этой совокупности решений не имеет. Итак, исходное уравнение имеет корни х1 и х2.

6. Уравнения вида

Уравнение

(15) где числа a, b, c, q, A таковы, что, не имеет корня х = 0, поэтому, разделив уравнение (15) на х2. получим равносильное ему уравнение, которое после замены неизвестной перепишется в виде квадратного уравнения, решение которого не представляет трудностей.

Пример 7. Решение уравнения

Решение. Так как х = 0 не является корнем уравнения (16), то, разделив обе его части на х2, получим уравнение

, (17) равносильное уравнению (16). Сделав замену неизвестной, уравнение (17) перепишем в виде

Квадратное уравнение (18) имеет 2 корня: у1 = 1 и у2 = -1. Поэтому уравнение (17) равносильно совокупности уравнений и (19)

Совокупность уравнений (19) имеет 4 корня: ,.

Они будут корнями уравнения (16).

§4. Рациональные уравнения

Уравнения вида = 0, где Н(х) и Q(x) – многочлены, называются рациональными.

Найдя корни уравнения Н(х) = 0, затем надо проверить, какие из них не являются корнями уравнения Q(x) = 0. Эти корни и только они будут решениями уравнения.

Рассмотрим некоторые методы решения уравнения вида = 0.

1. Уравнения вида

Уравнение

(1) при некоторых условиях на числа может быть решено следующим образом. Группируя члены уравнения (1) по два и суммируя каждую пару, надо получить в числителе многочлены первой или нулевой степени, отличающиеся только числовыми множителями, а в знаменателях – трехчлены с одинаковыми двумя членами, содержащими х, тогда после замены переменных получение уравнение будет либо иметь также вид (1), но с меньшим числом слагаемых, либо будет равносильно совокупности двух уравнений, одно из которых будет первой степени, а второе будет уравнением вида (1), но с меньшим числом слагаемых.

Пример. Решить уравнение

Решение. Сгруппировав в левой части уравнения (2) первый член с последним, а второй с предпоследним, перепишем уравнение (2) в виде

Суммируя в каждой скобке слагаемые, перепишем уравнение (3) в виде

Так как не есть решение уравнения (4), то, разделив это уравнение на, получим уравнение

, (5) равносильное уравнению (4). Сделаем замену неизвестного, тогда уравнение (5) перепишется в виде

Таким образом, решение уравнения (2) с пятью слагаемыми в левой части сведено к решению уравнения (6) того же вида, но с тремя слагаемыми в левой части. Суммируя все члены в левой части уравнения (6), перепишем его в виде

Решения уравнения есть и. Ни одно из этих чисел не обращает в нуль знаменатель рациональной функции в левой части уравнения (7). Следовательно, уравнение (7) имеет эти два корня, и поэтому исходное уравнение (2) равносильно совокупности уравнений

Решения первого уравнения этой совокупности есть

Решения второго уравнения из этой совокупности есть

Поэтому исходное уравнение имеет корни

2. Уравнения вида

Уравнение

(8) при некоторых условиях на числа можно решить так: надо выделить целую часть в каждой из дробей уравнения, т. е. заменить уравнение (8) уравнением

Свести его к виду (1) и затем решить его способом, описанным в предыдущем пункте.

Пример. Решить уравнение

Решение. Запишем уравнение (9) в виде или в виде

Суммируя слагаемые в скобках, перепишем уравнение (10) в виде

Делая замену неизвестного, перепишем уравнение (11) в виде

Суммируя члены в левой части уравнения (12), перепишем его в виде

Легко видеть, что уравнение (13) имеет два корня: и. Следовательно, исходное уравнение (9) имеет четыре корня:

3) Уравнения вида.

Уравнение вида (14) при некоторых условиях на числа можно решать так: разложив (если это, конечно, возможно) каждую из дробей в левой части уравнения (14) в суму простейших дробей

Свести уравнение (14) к виду (1), затем, проведя удобную перегруппировку членов полученного уравнения, решать его методом, изложенном в пункте 1).

Пример. Решить уравнение

Решение. Поскольку и, то, умножив числитель каждой дроби в уравнении (15) на 2 и заметив, что уравнение (15) можно записать в виде

Уравнение (16) имеет вид (7). Перегруппировав слагаемые в этом уравнении, перепишем его в виде или в виде

Уравнение (17) равносильно совокупности уравнений и

Для решения второго уравнения совокупности (18) сделаем замену неизвестного Тогда оно перепишется в виде или в виде

Суммируя все члены в левой части уравнения (19),перепишите его в виде

Так как уравнение не имеет корней, то уравнение (20) их также не имеет.

Первое уравнение совокупности (18) имеет единственный корень Поскольку этот корень входит в ОДЗ второго уравнения совокупности (18), то он является единственным корнем совокупности (18), а значит, и исходного уравнения.

4. Уравнения вида

Уравнение

(21) при некоторых условиях на числа и A после представления каждого слагаемого в левой части в виде может быть сведено к виду (1).

Пример. Решить уравнение

Решение. Перепишем уравнение (22) в виде или в виде

Таким образом, уравнение (23) сведено к виду (1). Теперь, группируя первый член с последним, а второй с третьим, перепишем уравнение (23) в виде

Это уравнение равносильно совокупности уравнений и. (24)

Последнее уравнение совокупности (24) можно переписать в виде

Решения этого уравнения есть и, так как входит в ОДЗ второго уравнения совокупности (30), то совокупность (24) имеет три корня:. Все они есть решения исходного уравнения.

5. Уравнения вида.

Уравнение вида (25)

При некоторых условиях на числа заменой неизвестного можно свести к уравнению вида

Пример. Решить уравнение

Решение. Так как не является решением уравнения (26), то разделив числитель и знаменатель каждой дроби в левой части на, перепишем его в виде

Сделав замену переменных перепишем уравнение (27) в виде

Решая уравнение (28) есть и. Поэтому уравнение (27) равносильно совокупности уравнений и. (29)

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF

Введение

Решение алгебраических уравнений высших степеней с одним неизвестным представляет собой одну из труднейших и древнейших математических задач. Этими задачами занимались самые выдающиеся математики древности.

Решение уравнений n-ой степени является важной задачей и для современной математики. Интерес к ним достаточно велик, так как эти уравнения тесно связаны с поиском корней уравнений, не рассматриваемых школьной программой по математике.

Проблема: отсутствие навыков решения уравнений высших степеней различными способами у учащихся мешает им успешно подготовиться к итоговой аттестации по математике и математическим олимпиадам, обучению в профильном математическом классе.

Перечисленные факты определили актуальность нашей работы «Решение уравнений высших степеней».

Владение простейшими способами решения уравнений n-ой степени сокращает время для выполнения задания, от которого зависит результат работы и качество процесса обучения.

Цель работы: изучение известных способов решения уравнений высших степеней и выявление наиболее доступных из них для практического применения.

Исходя из поставленной цели, в работе определены следующие задачи:

Изучить литературу и Интернет-ресурсы по данной теме;

Познакомиться с историческими фактами, касающимися данной темы;

Описать различные способы решения уравнений высших степеней

сравнить степень сложности каждого из них;

Познакомить одноклассников со способами решения уравнений высших степеней;

Создать подборку уравнений для практического применения каждого из рассмотренных способов.

Объект исследования - уравнения высших степеней с одной переменной.

Предмет исследования - способы решения уравнений высших степеней.

Гипотеза: общего способа и единого алгоритма, позволяющего за конечное число шагов находить решения уравнений n-ой степени, не существует.

Методы исследования:

- библиографический метод (анализ литературы по теме исследования);

- метод классификации;

- метод качественного анализа.

Теоретическая значимость исследования состоит в систематизации способов решения уравнений высших степеней и описании их алгоритмов.

Практическая значимость - предъявленный материал по данной теме и разработка учебного пособия для учащихся по данной теме.

1.УРАВНЕНИЯ ВЫСШИХ СТЕПЕНЕЙ

1.1 Понятие уравнения n-ой степени

Определение 1. Уравнением n-ой степени называется уравнение вида

a 0 xⁿ+a 1 x n -1 +a 2 xⁿ - ²+…+a n -1 x+a n = 0, где коэффициенты a 0, a 1, a 2…, a n -1, a n- любые действительные числа, причём,a 0 ≠ 0 .

Многочлен a 0 xⁿ+a 1 x n -1 +a 2 xⁿ - ²+…+a n -1 x+a n называют многочленом n-ой степени. Коэффициенты различают по названиям: a 0 - старший коэффициент; a n- свободный член.

Определение 2. Решениями или корнями для данного уравнения являются все значения переменной х , которые обращают это уравнение в верное числовое равенство или, при котором многочлен a 0 xⁿ+a 1 x n -1 +a 2 xⁿ - ²+…+a n -1 x+a n обращается в нуль. Такое значение переменной х называют также корнем многочлена. Решить уравнение - это значит найти все его корни или установить, что их нет.

Если a 0 = 1, то такое уравнение называют приведенным целым рациональным уравнением n-й степени.

Для уравнений третьей и четвёртой степени существуют формулы Кардано и Феррари, выражающими корни этих уравнений через радикалы. Выяснилось, что на практике ими редко пользуются. Таким образом, если n ≥ 3, а коэффициенты многочлена произвольные действительные числа, то поиск корней уравнения − задача непростая. Тем не менее, во многих частных случаях эта задача решается до конца. Остановимся на некоторых из них.

1.2 Исторические факты решения уравнений высших степеней

Уже в древности люди осознали, как важно научиться решать алгебраические уравнения. Около 4000 лет назад вавилонские ученые владели решением квадратного уравнения и решали системы двух уравнений, из которых одно - второй степени. С помощью уравнений высших степеней решались разнообразные задачи землемерия, архитектуры и военного дела, к ним сводились многие и разнообразные вопросы практики и естествознания, так как точный язык математики позволяет просто выразить факты и соотношения, которые, будучи изложенными обычным языком, могут показаться запутанными и сложными.

Универсальной формулы для нахождения корней алгебраического уравнения n-ой степени нет. Многим, разумеется, приходила в голову заманчивая мысль найти для любой степени n формулы, которые выражали бы корни уравнения через его коэффициенты, то есть, решали бы уравнение в радикалах.

Только в 16 веке итальянским математикам удалось продвинуться дальше - найти формулы для n= 3 и n= 4. Одновременно вопросом об общем решении уравнений 3-й степени занимались Сципион, Даль, Ферро и его ученики Фиори и Тарталья.

В 1545 году вышла книга итальянского математика Д. Кардано «Великое искусство, или о правилах алгебры», где наряду с другими вопросами алгебры рассматриваются общие способы решения кубических уравнений, а также метод решения уравнений 4-й степени, открытый его учеником Л. Феррари .

Полное изложение вопросов, связанных с решением уравнений 3-й и 4-й степеней, дал Ф. Виет.

В 20-х годах 19 века, норвежский математик Н. Абель доказал, что корни уравнений пятой степени не могут быть выражены через радикалы .

В ходе исследования было выявлено, что современной науке известно множество способов решения уравнений n-ой степени.

Результатом поиска методов решения уравнений высших степеней, неподдающихся решению способами, рассматриваемыми в школьной программе, стали способы, основанные на применении теоремы Виета (для уравнений степени n>2 ), теоремы Безу, схемы Горнера, а также формула Кардано и Феррари для решения кубических уравнений и уравнений четвертой степени.

В работе представлены методы решения уравнений и их виды, которые для нас стали открытием. К ним можно отнести - метод неопределенных коэффициентов, выделение полной степени, симметрические уравнения.

2. РЕШЕНИЕ ЦЕЛЫХ УРАВНЕНИЙ ВЫСШИХ СТЕПЕНЕЙ С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ

2.1 Решение уравнений 3-ей степени. Формула Д. Кардано

Рассмотрим уравнения вида x 3 +px+q=0. Преобразуем уравнение общего вида к виду: x 3 +px 2 +qx+r=0. Запишем формулу куба суммы; Сложим с первоначальным равенством и заменим на y . Получим уравнение: y 3 + (q -) (y -) + (r - =0. После преобразований, имеем: y 2 +py + q=0. Теперь, снова запишем формулу куба суммы:

(a + b ) 3 =a 3 + 3a 2 b + 3ab 2 + b 3 = a 3 + b 3 + 3ab (a + b), заменим (a + b )на x , получим уравнение x 3 - 3abx - (a 3 +b 3) = 0. Теперь видно, что исходное уравнение равносильно системе: и Решая систему, получим:

Мы получили формулу для решения приведенного уравнения 3-й степени. Она носит имя итальянского математика Кардано.

Рассмотрим пример. Решить уравнение: .

Имеем р = 15 и q = 124, тогда используя формулу Кардано вычислим корень уравнения

Вывод: данная формула хороша, но не подходит для решения всех кубических уравнений. Вместе с тем она громоздка. Поэтому на практике ею пользуются редко.

Но тот, кто овладеет данной формулой, может использовать её при решении уравнений третьей степени на ЕГЭ.

2.2 Теорема Виета

Из курса математики мы знаем данную теорему для квадратного уравнения, но мало кто знает, что ее используют и для решения уравнений высших степеней.

Рассмотрим уравнение:

разложим левую часть уравнения на множители, разделим на ≠ 0.

Правую часть уравнения преобразуем к виду

; отсюда следует, можно записать в систему следующие равенства:

Формулы, выведенные Виетом для квадратных уравнений и продемонстрированные нами для уравнений 3-й степени, верны и для многочленов высших степеней.

Решим кубическое уравнение:

Вывод: данный способ универсален и достаточно легок для понимания учащимися, так как теорема Виета им знакома по школьной программе для n = 2. Вместе с тем, чтобы находить корни уравнений с помощью данной теоремы необходимо обладать хорошими вычислительными навыками.

2.3 Теорема Безу

Эта теорема, названа по имени французского математика XVIII века Ж. Безу.

Теорема. Если уравнение a 0 xⁿ+a 1 x n -1 +a 2 xⁿ - ²+…+a n -1 x+a n = 0, в котором все коэффициенты целые числа, причем свободный член отличен от нуля, имеет целый корень, то этот корень является делителем свободного члена.

Учитывая, что в левой части уравнения многочлен n-й степени, то теорема имеет и другую трактовку.

Теорема. При делении многочлена n-й степени относительно x на двучлен x - a остаток равен значению делимого при x = a . (буква a может обозначать любое действительное или мнимое число, т.е. любое комплексное число) .

Доказательство: пусть f(x ) обозначает собой произвольный многочлен n-й степени относительно переменной x и пусть при его делении на двучлен (x-a ) получилось в частном q(x ), а в остатке R . Очевидно, что q(x) будет некоторый многочлен (n- 1)-й степени относительно x , а остаток R будет величиной постоянной, т.е. не зависящей от x .

Если бы остаток R был многочленом первой степени относительно x, то это означало бы, что деление не выполнено. Итак, R от x не зависит. По определению деления получаем тождество: f(x)=(x-a) q(x)+R .

Равенство справедливо при всяком значении x, значит, оно справедливо и при x=a , получим: f(a)=(a-a) q(a)+R . Символ f(a ) обозначает собой значение многочлена f(x ) при x=a, q(a) обозначает значение q(x ) при x=a. Остаток R остался таким, каким он был раньше, так как R от x не зависит. Произведение (x-a) q(a) = 0 , так как множитель (x-a) = 0, а множитель q(a) есть определенное число. Поэтому из равенства получим: f(a)= R, ч.т.д.

Пример 1. Найти остаток от деления многочлена x 3 - 3x 2 + 6x- 5 на двучлен

x- 2. По теореме Безу: R=f (2) = 23-322 + 62 -5=3. Ответ: R= 3.

Отметим, что теорема Безу важна не столь сама по себе, сколько своими следствиями. (Приложение 1)

Остановимся на рассмотрении некоторых приемов применения теоремы Безу к решению практических задач. Следует отметить, что при решении уравнений с помощью теоремы Безу необходимо:

Найти все целые делители свободного члена;

Из этих делителей найти хотя бы один корень уравнения;

Левую часть уравнения разделить на (х-а );

Записать в левой части уравнения произведение делителя и частного;

Решить полученное уравнение.

Рассмотрим на примере решения уравнения х 3 + 4х 2 + х - 6 = 0 .

Решение:находим делители свободного члена ±1; ± 2; ± 3; ± 6. Вычислим значения при х= 1, 1 3 + 41 2 + 1- 6=0. Разделим левую часть уравнения на (х- 1). Деление выполним «уголком», получим:

Вывод: теорема Безу один из тех способов, которые мы рассматриваем в нашей работе, изучается в программе факультативных занятий. Она трудна в понимании, потому что, чтобы ей владеть, надо знать все следствия из нее, но при этом теорема Безу является одним из главных помощников учащихся на ЕГЭ.

2.4 Схема Горнера

Для деления многочлена на двучлен х-α можно использовать специальный несложный прием, придуманный английскими математиками XVII века, впоследствии названной схемой Горнера. Помимо нахождения корней уравнений, по схеме Горнера можно более просто вычислять их значения. Для этого необходимо подставить значение переменной в многочлен Pn(x)=a 0 xn+a 1 x n-1 +a 2 xⁿ - ²+…++ a n -1 x+a n. (1)

Рассмотрим деление многочлена (1) на двучлен x -α.

Выразим коэффициенты неполного частного b 0 xⁿ - ¹+ b 1 xⁿ - ²+ b 2 xⁿ - ³+…+ bn -1 и остаток r через коэффициенты многочлена Pn(x ) и число α. b 0 =a 0 , b 1 = α b 0 +a 1 , b 2 = α b 1 +a 2 …, bn -1 =

= α bn -2 +a n -1 = α bn -1 +a n .

Вычисления по схеме Горнера представлены в виде следующей таблицы:

Поскольку r=Pn(α), то α − корень уравнения. Для того чтобы проверить не является ли α кратным корнем, схему Горнера можно применить уже к частному b 0 x+ b 1 x+…+ bn -1 по таблице. Если в столбце под bn -1 получится снова 0, значит α − кратный корень.

Рассмотрим пример: решить уравнение х 3 + 4х 2 + х - 6 = 0.

Применим к левой части уравнения разложение на множители многочлена, стоящего в левой части уравнения, схему Горнера.

Решение:находим делители свободного члена ± 1; ± 2; ± 3; ± 6.

Коэффициенты частного - числа 1, 5, 6, а остаток r = 0.

Значит, х 3 + 4х 2 + х - 6 = (х - 1) (х 2 + 5х + 6) = 0.

Отсюда: х - 1 = 0 или х 2 + 5х + 6 = 0.

х = 1, х 1 = -2; х 2 = -3. Ответ: 1,- 2, - 3.

Вывод: таким образом, на одном уравнении мы показали применение двух различных способов разложения на множители многочленов. На наш взгляд, схема Горнера наиболее практична и экономична.

2.5 Решение уравнений 4-ой степени. Метод Феррари

Ученик Кардано Людовик Феррари обнаружил способ решения уравнения 4-й степени. Метод Феррари состоит из двух этапов.

I этап: уравнения вида представляется в виде произведения двух квадратных трехчленов это следует из того, что уравнение 3-ей степени и хотя бы одно решение.

II этап: полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.

Идея в том, чтобы представить уравнения в виде A 2 =B 2 , где A=x 2 +s,

B-линейная функция от x . Тогда остаётся решить уравнения A = ±B.

Для наглядности рассмотрим уравнение: Уединим 4-ю степень, получим: Для любого d выражение будет полным квадратом. Прибавим к обеим частям уравнения получим

В левой части полный квадрат, можно подобрать d , чтобы и правая часть (2) стала полным квадратом. Представим себе, что мы достигли этого. Тогда наше уравнение выглядит так:

Найти корень впоследствии не составит никакого труда. Чтобы правильно подобрать d надо, чтобы дискриминант правой части (3) обратился в нуль, т.е.

Итак, чтобы найти d , надо решить это уравнение 3-й степени. Такое вспомогательное уравнение называют резольвентой .

Легко находим целый корень резольвенты: d = 1

Подставив в (1) уравнение получим

Вывод: метод Феррари универсален, но сложен и громоздкий. Вместе с тем, если алгоритм решения понятен, то уравнения 4-й степени можно решать данным методом.

2.6 Метод неопределенных коэффициентов

Успех решения уравнения 4-й степени методом Феррари зависит от того, реши ли мы резольвенту - уравнение 3-й степени, что как мы знаем, не всегда удается.

Суть метода неопределенных коэффициентов состоит в том, что вид сомножителей, на которые разлагается данный многочлен, угадывается, а коэффициенты этих сомножителей (также многочленов) определяется путем перемножения сомножителей и приравнивания коэффициентов при одинаковых степенях переменной .

Пример: решите уравнение:

Предположим, что левую часть нашего уравнения можно разложить на два квадратных трехчлена с целыми коэффициентами такие, что справедливо тождественное равенство

Очевидно, что коэффициенты перед уних должны быть равными 1, а свободные члены - у одного + 1, у другого - 1.

Неопределенными остаются коэффициенты, стоящие перед х . Обозначим их через а и и чтобы их определить, перемножим оба трехчлена правой части уравнения.

В результате получим:

Приравнивая коэффициенты при одинаковых степенях х в левой и правой частях равенства (1), получаем систему для нахождения и

Решив эту систему, будем иметь

Итак, наше уравнение равносильно уравнению

Решив его, получаем следующие корни: .

Метод неопределенных коэффициентов опирается на следующие утверждения: любой многочлен четвертой степени, стоящий в уравнении, можно разложить на произведение двух многочленов второй степени; два многочлена тождественно равны тогда и только тогда, когда равны их коэффициенты при одинаковых степенях х.

2.7 Симметрические уравнения

Определение. Уравнение вида называется симметрическим, еслипервые коэффициенты, стоящие в уравнении слева, равны первым коэффициентам, стоящим справа .

Мы видим, что первые коэффициенты слева равны первым коэффициентам справа.

Если такое уравнение имеет нечетную степень, то оно имеет корень х = - 1. Далее мы можем понизить степень уравнения, поделив его на (х+ 1). Оказывается, что при делении симметрического уравнения на (х+ 1) получается симметрическое уравнение четной степени. Доказательство симметричности коэффициентов представлено ниже. (Приложение 6) Наша задача - научиться решать симметрические уравнения четной степени.

Например: (1)

Решим уравнение (1), поделим на х 2 (на среднюю степень) = 0.

Сгруппируем слагаемые с симметричными

) + 3(x + . Обозначим у = x + , возведём обе части в квадрат, отсюда = у 2 Итак, 2(у 2 или 2у 2 + 3 решив уравнение, получим у = , у = 3. Далее вернёмся к замене x + = и x + = 3. Получим уравнения и Первое не имеет решения, а второе имеет два корня. Ответ:.

Вывод: данный вид уравнений не часто встречающийся, но если он вам попался, то его можно решить легко и просто не прибегая к громоздким вычислениям.

2.8 Выделение полной степени

Рассмотрим уравнение.

Левая часть представляет собой куб суммы (х+1), т.е.

Извлекаем корень третьей степени из обеих частей: , далее получим

Откуда единственный корень.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

По результатам работы мы пришли к следующим выводам:

Благодаря изученной теории мы познакомились с различными методами решения целых уравнений высших степеней;

Формула Д. Кардано является сложной в применении и даёт большую вероятность допустить ошибки при вычислении;

− метод Л. Феррари позволяет свести решение уравнения четвертой степени к кубическому;

− теорема Безу может применяться как для кубических уравнений, так и для уравнений четвертой степени; она более понятна и наглядна в применении к решению уравнений;

Схема Горнера помогает существенно сократить и упростить вычисления в решении уравнений. Помимо нахождения корней, по схеме Горнера можно более просто вычислять значения многочленов, стоящих в левой части уравнения;

Особый интерес вызвали решения уравнений методом неопределённых коэффициентов, решение симметрических уравнений.

В ходе исследовательской работы было выяснено, что с простейшими способами решения уравнений высшей степени учащиеся знакомятся на занятиях факультатива по математике, начиная с 9-го или 10-го классов, а также на спецкурсах выездных математических школ. Данный факт установлен в результате опроса учителей математики МБОУ «СОШ № 9» и учащихся, проявляющих повышенный интерес к предмету «математика».

Наиболее востребованными методами решения уравнений высших степеней, которые встречаются при решении олимпиадных, конкурсных задач и в результате подготовки к экзаменам учащимися, являются методы, основанные на применении теоремы Безу, схемы Горнера и введение новой переменной.

Демонстрация результатов исследовательской работы, т.е. способов решения уравнений, не изучаемых в школьной программе по математике, заинтересовала одноклассников.

Заключение

Изучив учебную и научную литературу, Интернет-ресурсы в молодежных образовательных форумах